基数排序

计数排序的稳定版本

在学习基数排序之前，需要先了解计数排序的稳定版本。

之前了解的计数排序，只是朴素版的计数排序，除此之外，还有稳定版的计数排序。

朴素版的计数排序，只是给整数进行排序，当然没有什么问题，但是在一些给学生考试分数排序类似的场景中，这种要求保证排序后，数组中相等元素原本的先后顺序不变的，举个例子，也就是说，对于两个相同的数来说，在输入数组中先出现的数，在输出数组中也位于前面。

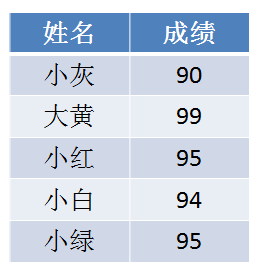
成绩表，图源自小灰的文章

如果是朴素版的计数排序，计数数组得到的结果是这样的。

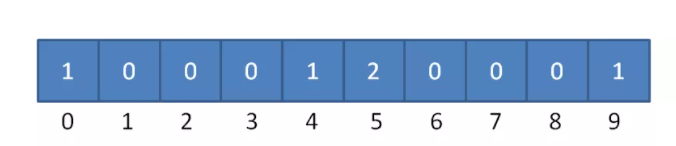
朴素版计数排序得到的计数数组，图源自小灰的文章

而如果是稳定版的计数排序，计数数组会从第二个元素开始，每个元素都加上前面的所有元素之和。

这样做的目的是让计数数组中存储的数值，等于相应整数的最终排序位置。

比如下图中，下标为9的数值是5，代表整数9的排序位置为第5位。

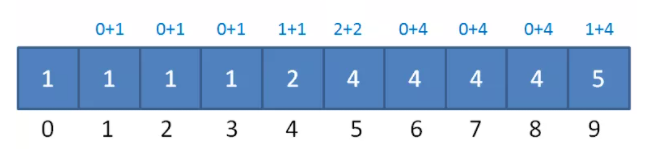
稳定版计数排序得到的计数数组，图源自小灰的文章

接着创建一个输出数组，与需要排序的数值数组大小一致，再遍历开头的成绩表，从后向前得到所有成绩单的名次。

小绿成绩是95，则计数数组中下标为5的值——4，排名4就是小绿的名次，将小绿结果写入结果数组，并将计数数组下标5的值进行减1(代表假如下次遇到相同成绩时，排名为4-1=3)

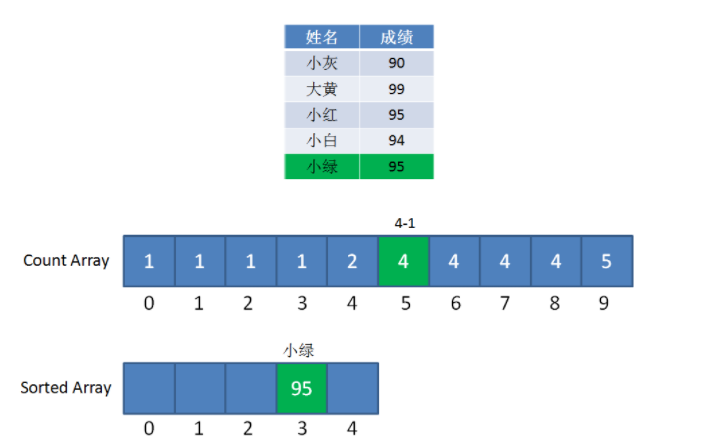
小绿成绩排序，图源自小灰的文章

小白成绩是94，则计数数组中下标为4的值——2，排名2就是小白的名次，将小白结果写入结果数组，并将计数数组下标4的值进行减1(代表假如下次遇到相同成绩时，排名为2-1=1)

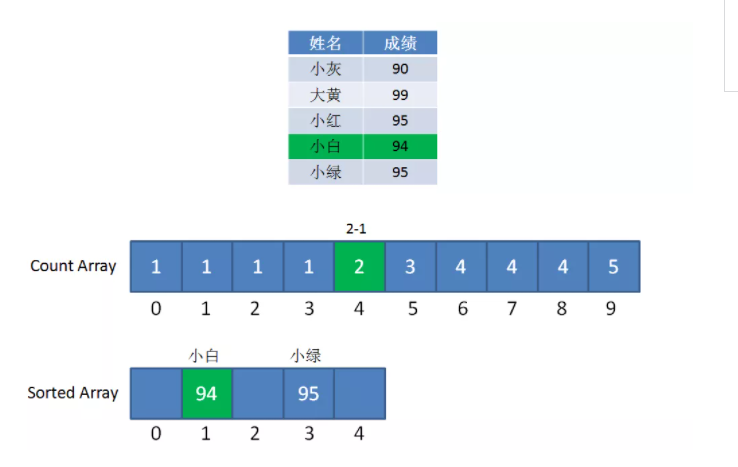
小白成绩排序，图源自小灰的文章

后续遍历过程以此类推，最后就能得到小红和小绿清楚的排序了。

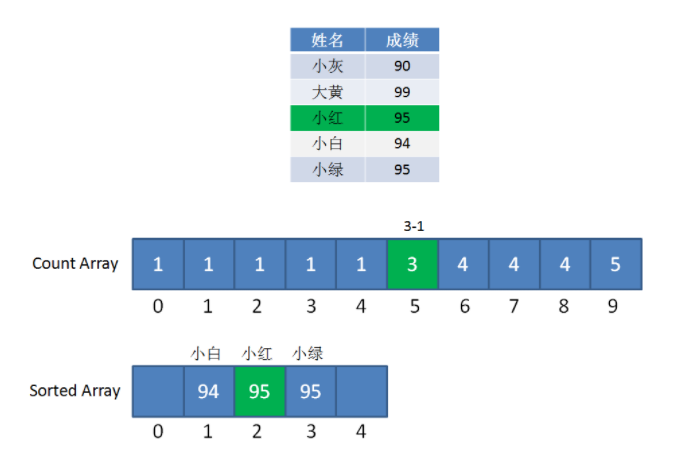
小红和小绿的排序，图源自小灰的文章

以上便是计数排序的稳定版。

什么是基数排序

基数排序是按照数字的”位”，也称有效位和基数，来进行排序。

位是进制中的位，比如十进制的基数是10，百进制的基数是100……，所以我们才能按照个十百千万等的位来进行排序。

基数排序不仅可以为一组给定的手机号进行排序，也可以对英文单词进行排序。这些复杂的元素组合排序，基数排序会把排序工作拆分成多个阶段，每个阶段只对一个字符或数值进行计数排序，排序轮次跟元素长度相同。

例如有以下几个字母。

每轮分别对个位、十位、百位的字母(根据字母的ascii码数值大小)，每一位进行一次计数排序，就是基数排序的流程。这种基数排序也叫MSD(从高位优先进行排序)，同等的，另外还有一种称为LSD(从低位优先进行排序)。

如果遇到字符数量不同的单词，例如

// apple
// his
// movie
// age
// hi
// company

这里最长的单词，company，字符长度是7，则对其它不足字符长度7的单词末尾进行补零。

排序时，把0作为最小的数值即可。

// apple00
// his0000
// movie00
// age0000
// hi00000
// company

代码实现

/**
 * 找出数组的最大值
 * @param {array} array 要进行搜索的数组
 * @param {function} compareFn // 比较用的方法，默认为defaultCompare
 * @returns {number} 返回找到的数组最大值
 */
export function findMaxValue(array, compareFn = defaultCompare) {
  if (array && array.length > 0) {
    let max = array[0];
    for (let i = 1; i < array.length; i++) {
      if (compareFn(max, array[i]) === Compare.LESS_THAN) {
        max = array[i];
      }
    }
    return max;
  }
  return undefined;
}
/**
 * 找出数组的最小值
 * @param {array} array 要进行搜索的数组
 * @param {function} compareFn // 比较用的方法，默认为defaultCompare
 * @returns {number} 返回找到的数组最小值
 */
export function findMinValue(array, compareFn = defaultCompare) {
  if (array && array.length > 0) {
    let min = array[0];
    for (let i = 1; i < array.length; i++) {
      if (compareFn(min, array[i]) === Compare.BIGGER_THAN) {
        min = array[i];
      }
    }
    return min;
  }
  return undefined;
}
/**
 * 计算桶索引
 * @param {number} value 要获取位置的值
 * @param {number} minValue 数组中的最小值
 * @param {number} significantDigit 有效位
 * @param {number } radixBase 基数，10进制排序，默认基数为10
 * @return {number} 值对应桶区间的索引
 */
const getBucketIndex = (value, minValue, significantDigit, radixBase) =>
  // 将元素根据不同的区间跨度，分布到桶中
  Math.floor(((value - minValue) / significantDigit) % radixBase);

/**
 * 基于有效位（基数）排序（使用桶排序）
 * @param {array} array 要进行排序的数组
 * @param {number} radixBase 基数，10进制排序，默认基数为10
 * @param {number} significantDigit 有效位
 * @param {number} minValue 数组的最小值
 * @returns {array} 返回排序后的数组
 */
const countingSortForRadix = (array, radixBase, significantDigit, minValue) => {
  let bucketsIndex;
  const buckets = []; // 存储桶的变量
  const aux = [];
  // 通过radixBase来初始化桶，默认初始化为0
  for (let i = 0; i < radixBase; i++) { // 首先，我们基于基数初始化桶，由于我们排序的是十进制数，那么需要10个桶。
    buckets[i] = 0;
  }
  // 遍历array，基于有效位计算桶索引执行计数排序（计数排序的稳定排序)
  // 计数排序文章:https://mp.weixin.qq.com/s/WGqndkwLlzyVOHOdGK7X4Q
  for (let i = 0; i < array.length; i++) { // 然后，我们会基于数组中
    bucketsIndex = getBucketIndex(array[i], minValue, significantDigit, radixBase); // 计算桶索引
    buckets[bucketsIndex]++; // 根据桶索引，执行计数操作
  }
  for (let i = 1; i < radixBase; i++) { // 计算累积结果来得到正确的计数值，从1开始遍历到radixBase位置。
    buckets[i] += buckets[i - 1]; // 从第二个元素开始，每一个元素都加上前面所有元素之和。
  }
  // 计数完成，遍历array将值移回原始数组中，用aux辅助数组来存储
  for (let i = array.length - 1; i >= 0; i--) {   // 对原始数组中的每个值
    bucketsIndex = getBucketIndex(array[i], minValue, significantDigit, radixBase); // 计算当前元素的桶索引
    aux[--buckets[bucketsIndex]] = array[i]; // 对当前桶索引内的元素执行自减操作，得到其在数组中的正确位置index
  }
  //计算出索引后，在aux中的对应位置存储当前遍历到的元素
  for (let i = 0; i < array.length; i++) {
    array[i] = aux[i];
  }
  return array;
};
/**
 * 基数排序
 * 参考文章:https://juejin.cn/post/6860501233308794887#heading-31
 * @param {array} array 要进行排序的数组
 * @param {number} radixBase // 基数，10进制排序，默认基数为10
 * @returns {array} 返回排序后的数组
 */
export function radixSort(array, radixBase = 10) {
  // 如果array的长度小于2，则array不需要排序，直接返回
  if (array.length < 2) {
    return array;
  }
  /**
   * 这个算法也可以被修改成支持排序字母字符。我们首先只会基于最后一位有效位对数字进行排序，在下次迭代时，我们会基于第二个有效位进行排序（十位数字），然后是第三个有效位（百位数字），以此类推。我们继续这个过程直到没有待排序的有效位，这也是为什么我们需要知道数组中的最小值和最大值。
   */
  const minValue = findMinValue(array); // 获取array的最小值
  const maxValue = findMaxValue(array); // 获取array的最大值
  // 当前有效数字,默认会从最后一位（最低位）有效数字开始排序
  let significantDigit = 1;
  /**
  * 计算有效位
  * 最大值和最小值的差与有效位数字进行除法运算，其值大于等于1就代表还有待排序的有效位
  */
  while ((maxValue - minValue) / significantDigit >= 1) { // 计算有效位，如果(数组最大数 - 数组最小数) / 当前有效位的数字 >= 1
    // console.log('radix sort for digit ' + significantDigit);
    // 以当前有效位作为参数调用countingSortForRadix函数对数组进行排序
    array = countingSortForRadix(array, radixBase, significantDigit, minValue);
    // console.log(array.join());
    // 当前有效数字乘以基数，继续执行while循环进行基数排序
    significantDigit *= radixBase;
  }
  return array;
}