快速排序

什么是快速排序

和归并排序一样，快速排序也使用分而治之的算法。

快速排序是从冒泡排序演变过来的算法，但是快速排序性能远远优于冒泡排序。

快速排序的基本步骤：

  1. 快速排序会从数列中选择一个值作为基准元素(基准元素的挑选和作用，在”相关概念”中有介绍)
  2. 并创建双指针引用(左指针和右指针，在”相关概念”中有介绍)
  3. 移动左指针直到找到一个比基准元素大的值，接着，移动右指针直到找到一个比基准元素小的值，然后交换他们，不断重复这个过程，直到左指针超过了右指针。此时所有比基准元素小的值都排在了基准元素的左侧，比基准元素大的值都排在了基准元素的右侧。
  4. 接着进行划分操作——partition，算法对划分后的小数组（较主元小的值组成的子数组，以及较主元大的值组成的子数组）进行前面相同的步骤，直至数组已完全排序。

相关概念

基准元素

基准元素，英文pivot，快速排序会在每一轮挑选一个基准元素，作为分而治之法的中心，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成了两个部分。

基准元素如何选择呢？

基准元素的选择方式有很多，常见的有选择数列的第一个元素，数列中间的元素，甚至可以随机选择一个元素作为基准元素。

本文例子以数列中间的元素作为基准元素。

基准元素的选择没有绝对的好坏，取决于选择的基准元素，选到数列的最大值或最小值的概率，导致时间复杂度的变化。

快速排序的平均时间复杂度是 O（nlogn），最坏情况下的时间复杂度是 O（n^2）

左指针

快速排序使用双指针法，用于元素交换前的元素扫描，分为左指针和右指针。

左指针初始指向数列第一个元素，左指针目标是找到一个比基准元素要大的元素。

右指针

快速排序使用双指针法，用于元素交换前的元素扫描，分为左指针和右指针。

右指针初始指向数列最后一个元素，右指针目标是找到一个比基准元素要小的元素。

图解快速排序

假如对这样一组数列进行排序

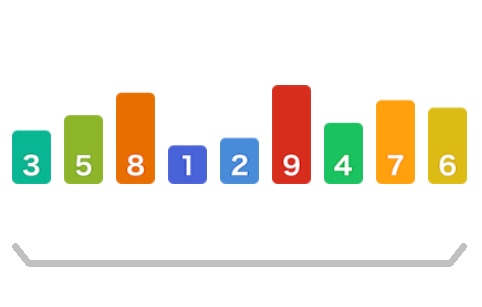
图解快速排序-1

选择最右边的数字作为基准元素(选择基准元素的方法有很多种，这只是其中一种)

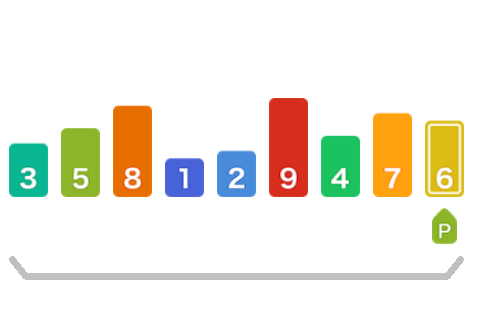
图解快速排序-2

并创建双指针引用，左指针初始指向数列第一个元素，右指针初始指向数列最后一个元素。

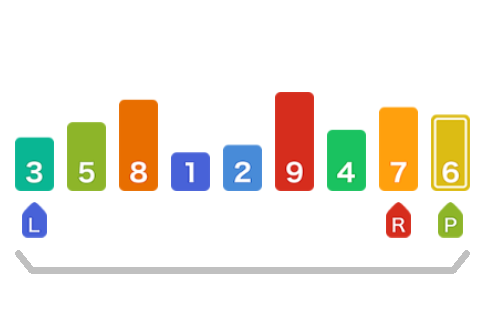
图解快速排序-3

移动左指针直到找到一个比基准元素大的值，此时找到8

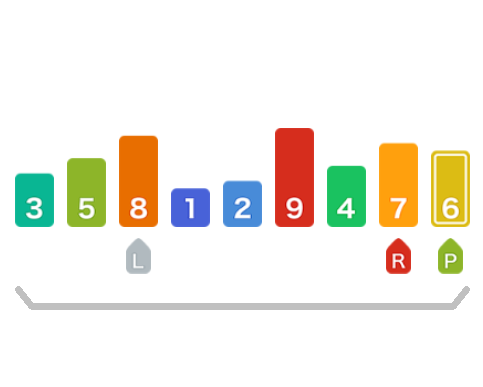
图解快速排序-4

移动右指针直到找到一个比基准元素小的值，此时找到4

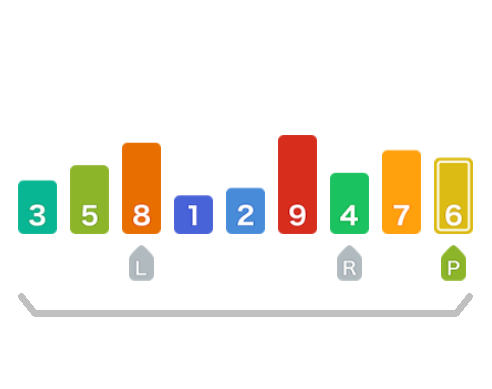
图解快速排序-5

然后交换他们，也就是交换8和4

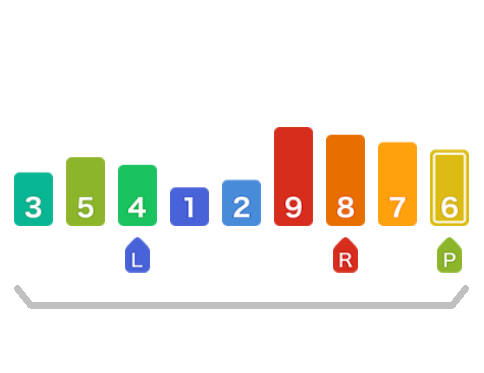
图解快速排序-6

重复相同的步骤，继续从左标记开始移动，直到找到一个比基准元素大的值，此时找到9

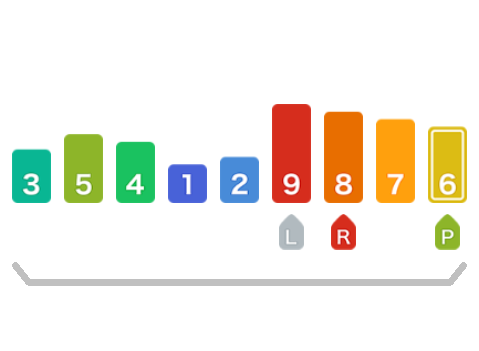
图解快速排序-7

从右标记开始移动，但是此时没有左右标记碰到了一起，也会停止移动，并交换这个数字与基准元素的位置。

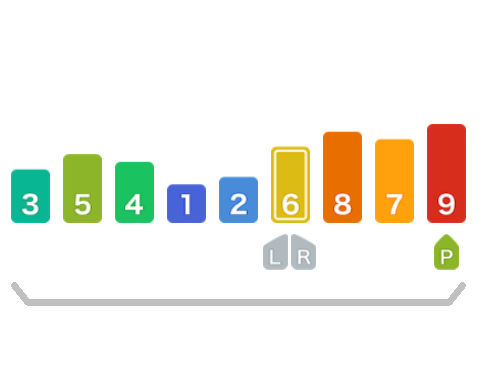
图解快速排序-8

此时所有比基准元素小的值都排在了基准元素的左侧，比基准元素大的值都排在了基准元素的右侧。

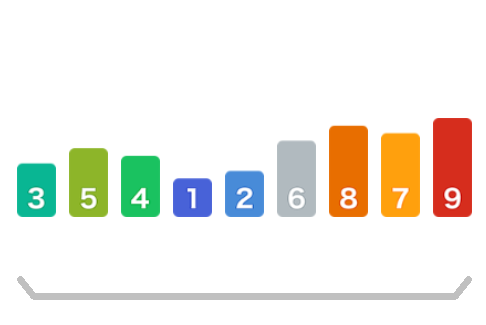
图解快速排序-9

接着进行划分操作——partition，把基准元素之前的元素划分为左侧子数组[3,5,4,1,2]，基准元素之后的元素划分为右侧子数组[8,7,9]，先对左侧子数组进行上述相同的操作。

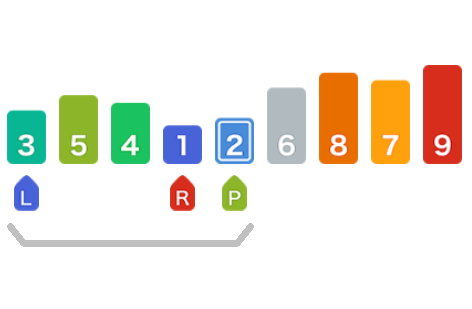
图解快速排序-10

此时操作后的左侧子数组也能拆出更小的子序列，在这里，左侧子数组为2之前的元素，右侧子数组为2之后，6之前的元素，也就是[4,3,5]。

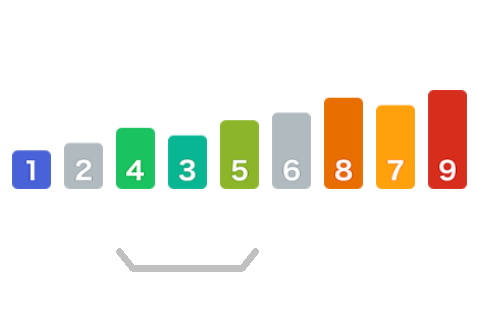
图解快速排序-11

因为左侧只有一个数字1，则认为已完成排序，不需要操作。此时操作右侧子数组[4,3,5]。

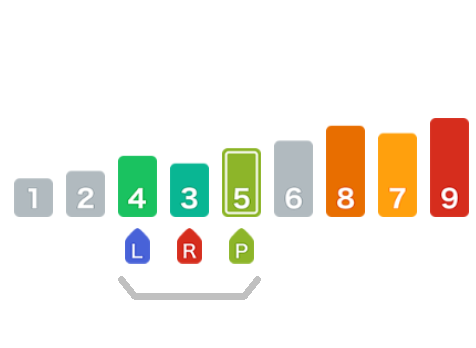
图解快速排序-12

也重复上述相同的操作，直至所有数字排序完成。

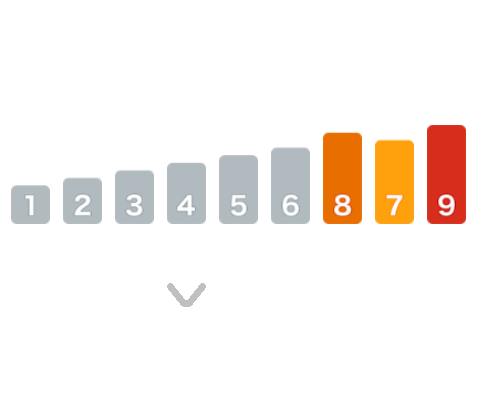
图解快速排序-13

操作完最外层的左侧子数组，则继续对右侧子数组进行上述相同的操作。

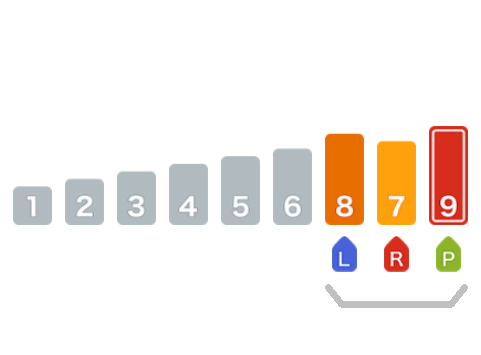
图解快速排序-14

最终所有数字完成排序。

图解快速排序-15

快速排序动画图解

快速排序动画图解

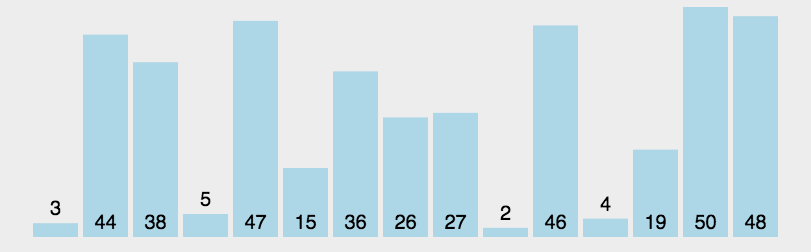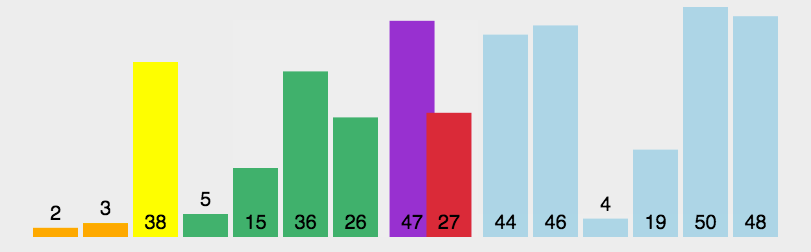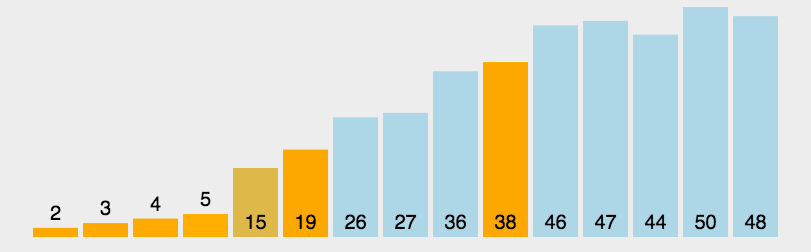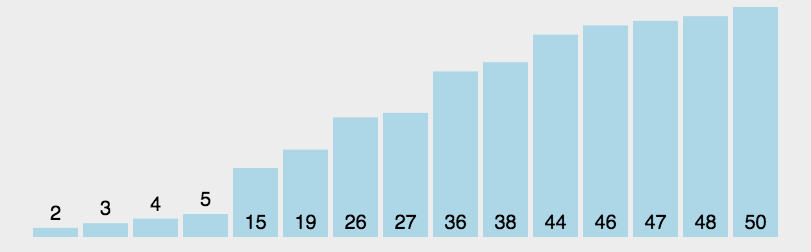
代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
// 比较用的常量对象(保证代码优雅)
export const Compare = {
  LESS_THAN: -1, // 如果第一个元素小于第二个元素，它就返回-1
  BIGGER_THAN: 1, // 如果第一个元素大于第二个元素，它就返回1
  EQUALS: 0 // 如果元素有相同的引用，它就返回 0
};
// 比较用的方法
export function defaultCompare(a, b) {
  // 如果元素有相同的引用，它就返回 0
  if (a === b) {
    return Compare.EQUALS;
  }
  // 如果第一个元素小于第二个元素，它就返回-1,否之返回1
  return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
/**
 * 交换函数
 * @param {*} array 传入需要交换的数组(这里传入堆)
 * @param {*} a 传入要交换的节点A
 * @param {*} b 传入要交换的节点B
 */
 export function swap(array, a, b) {
  // ES5写法(性能较好)
  /* const temp = array[a]; // 要交换数组中的两个值，我们需要一个辅助变量来复制要交换的第一个元素
  array[a] = array[b]; // 然后，将第二个元素赋值到第一个元素的位置
  array[b] = temp; */ // 最后，将复制的第一个元素的值覆盖到第二个元素的位置
  // ES6写法(性能较差) https://bugzilla.mozilla.org/show_bug.cgi?id=1177319
  [array[a], array[b]] = [array[b], array[a]];
}
/**
 * 快速排序进行划分过程(选择基准元素)的内部方法
 * 选择基准元素有好几种方法，比较常见的一种方法是选择数组中间的值
 * @param {array} array 要进行排序的数组
 * @param {array} left 左侧低指针
 * @param {array} right 右侧高指针
 * @param {function} compareFn // 比较用的方法，默认为defaultCompare
 * @returns {array} 返回排序后的数组
 */
function partition(array, left, right, compareFn) {
  const pivot = array[Math.floor((right + left) / 2)]; // 我们选择中间值作为基准元素
  let i = left; // left指针，初始化为数组第一个元素；
  let j = right;

  while (i <= j) { // 只要 left 和 right 指针没有相互交错，就执行划分操作。
    while (compareFn(array[i], pivot) === Compare.LESS_THAN) { // 首先，移动 left 指针直到找到一个比基准元素大的元素
      i++;
    }
    while (compareFn(array[j], pivot) === Compare.BIGGER_THAN) { // 对 right 指针，我们做同样的事情，移动 right指针直到我们找到一个比基准元素小的元素
      j--;
    }
    if (i <= j) { // 当左指针指向的元素比基准元素大且右指针指向的元素比基准元素小,并且此时左指针索引没有右指针索引大时(i <= j),此时左项比右项大（值比较）
      swap(array, i, j); // 我们交换它们
      // 然后移动两个指针，并重复此过程
      i++;
      j--;
    }
  }
  return i; // 在划分操作结束后，返回左指针的索引
}
/**
 * 快速排序的内部方法
 * @param {array} array 要进行排序的数组
 * @param {array} left 左侧低指针
 * @param {array} right 右侧高指针
 * @param {function} compareFn // 比较用的方法，默认为defaultCompare
 * @returns {array} 返回排序后的数组
 */
function quick(array, left, right, compareFn) {
  let index; // index变量能帮助我们将子数组分离为较小值数组和较大值数组。
  if (array.length > 1) { // 如果数组的长度比 1 大（因为只有一个元素的数组必然是已排序了的）
    index = partition(array, left, right, compareFn); // 我们将对给定子数组执行 划分(partition) 操作（第一次调用是针对整个数组）以得到 index
    if (left < index - 1) { // 如果子数组存在较小值的元素
      quick(array, left, index - 1, compareFn); // 则对该数组重复这个过程
    }
    // 同理，对存在较大值的子数组也是如此
    if (index < right) {  // 如果有子数组存在较大值
      quick(array, index, right, compareFn); // 我们也将重复快速排序过程
    }
  }
  return array;
}
/**
 * 快速排序
 * @param {array} array 要进行排序的数组
 * @param {function} compareFn // 比较用的方法，默认为defaultCompare
 * @returns {array} 返回排序后的数组
 */
export function quickSort(array, compareFn = defaultCompare) {
  return quick(array, 0, array.length - 1, compareFn);
}
算法
快速排序
https://sothx.com/2021/04/27/quickSort/
作者
Sothx
发布于
2021年4月27日
许可协议