归并排序

什么是分而治之

在学习归并排序之前，需要先了解一下什么是分而治之。

分而治之是算法设计中的一种思想。它将一个问题分成多个和原问题相似的小问题，递归解决小问题， 再将解决方式合并以解决原来的问题。

分而治之算法的三部分：

1. 分解原问题为多个子问题（原问题的多个小实例）。
2. 解决子问题，用返回解决子问题的方式的递归算法。递归算法的基本情形可以用来解决子问题。
3. 组合这些子问题的解决方式，得到原问题的解。

什么是归并排序

归并排序是一种分而治之的算法。

所以，归并排序的基本思想也同上面分而治之算法的三部分一致：

1. 将原始数组切分成较小的数组
2. 直到每个小数组只有一个位置的大小(也就是把数组长度为1)，接着将小数组归并成较大的数组
3. 直到最后只有一个排序完毕的大数组

图解归并排序

假设有这样一组数字需要排序。

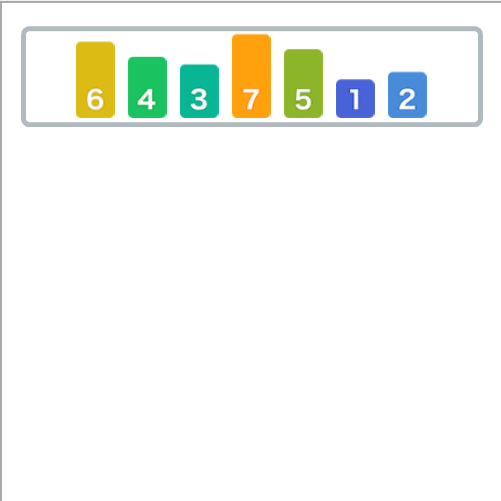
首先，我们将数字分成两半。

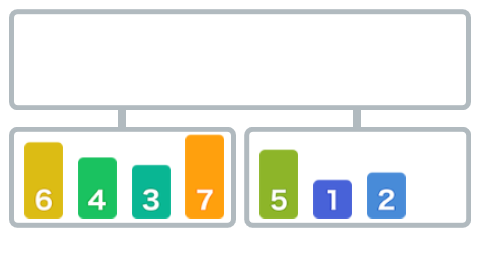
再继续将数字序列对半分割。

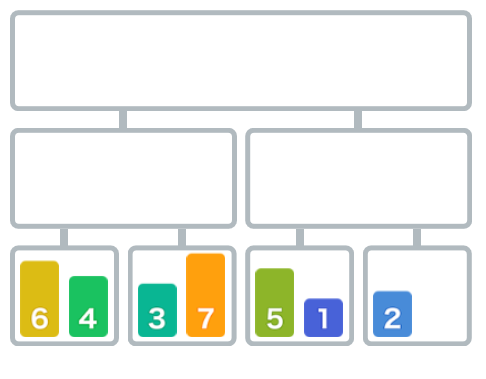
再继续分割，直到每个小数组只有一个位置的大小(也就是把数组长度为1)，分割完毕。

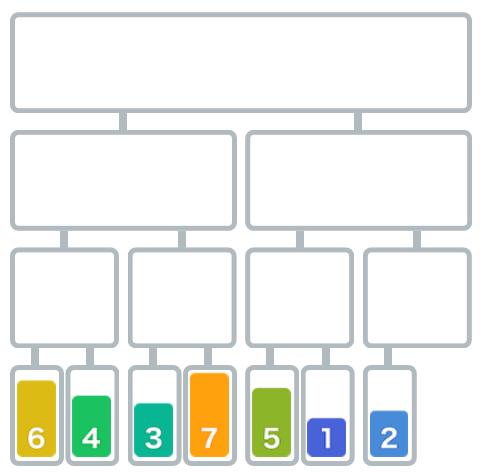
接下来，对分割后的元素进行合并。(合并假设按照升序排列)

将6与4进行合并，按升序规则，6比4大，先移动4，再移动6，合并后的顺序为[4,6]

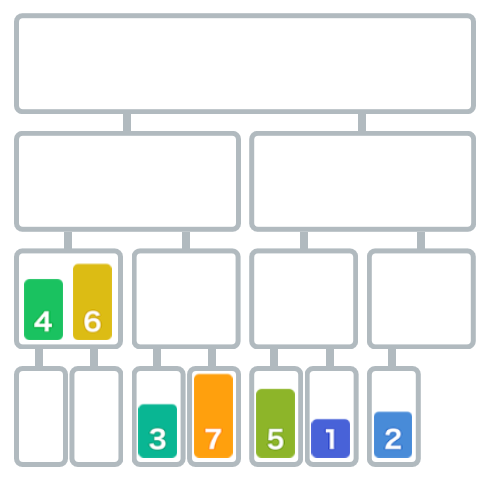
接下来把3和7进行合并，3比7小，可以直接合并，合并后的顺序为[3,7]

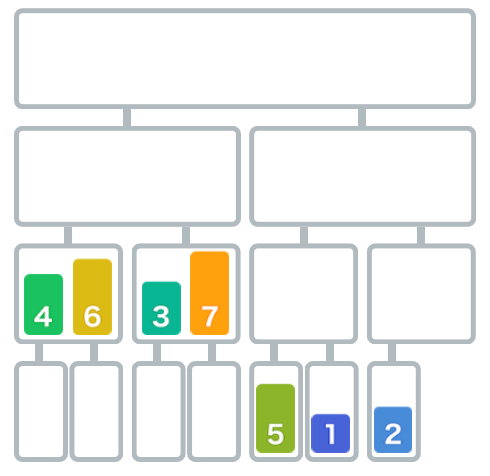
此时，已经产生了两组从小到大排列的数据[4,6]和[3,7]，符合了归并的要求，将这两组数据代入归并中，进行合并。

由于他们两个数据均是包含多个数字的组，则从开头的数字开始比较。

在图中，比较开头的4和3，4大于3，所以移动3。

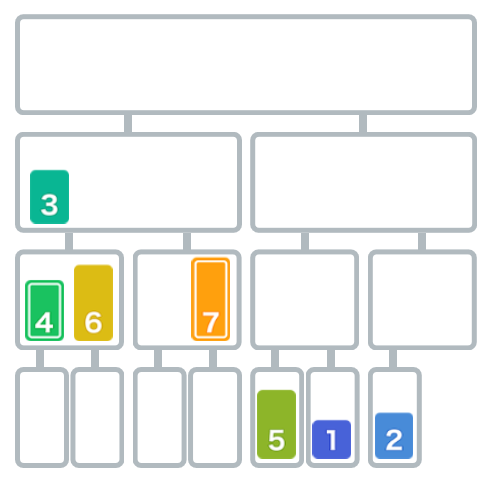
再从开头比较剩余的数字，在图中，比较4和7。

4小于7，所以移动4。

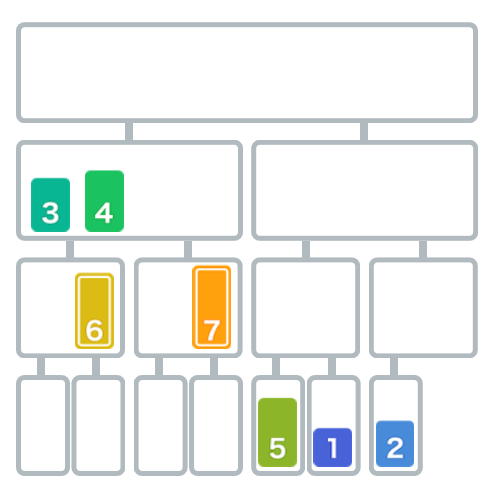
比较6和7，6小于7，移动6。

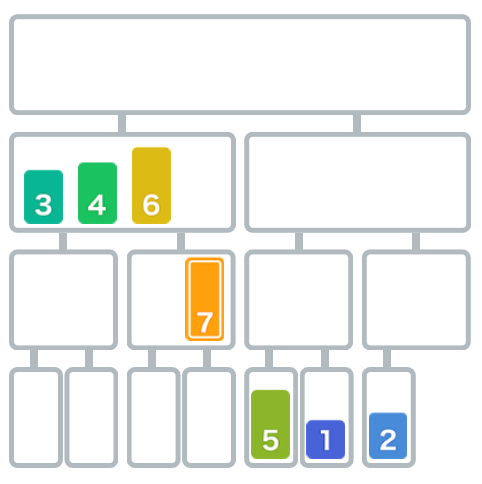
移动剩下的7。

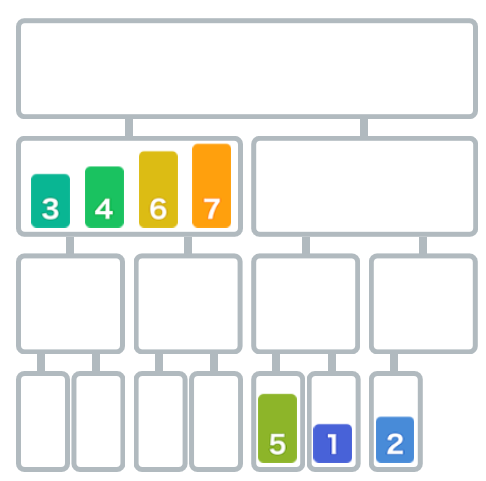
此时右边还有未递归合并的组，也像上方相同的操作对数字进行合并。

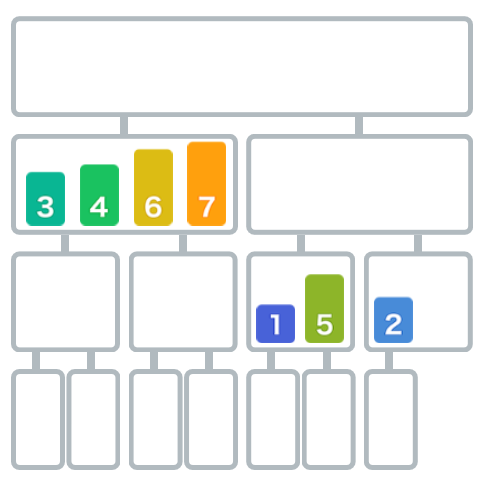
再继续对右边子数组进行合并。

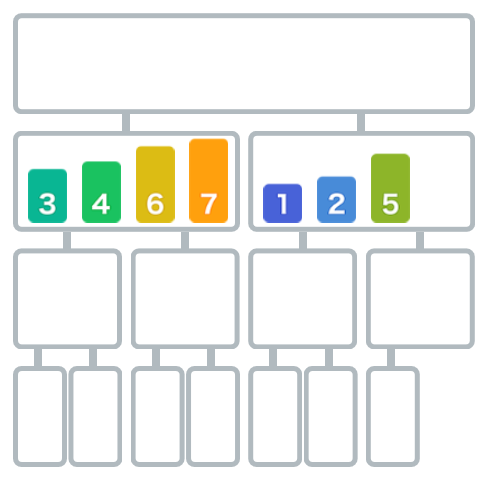
同样进行合并，直到所有数字都在一个组中，此时归并排序完成。

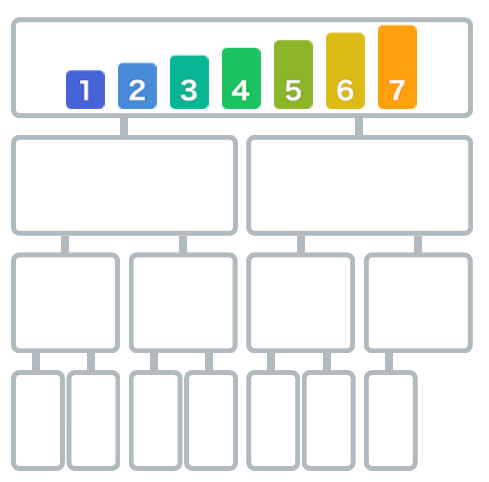
动画图解归并排序

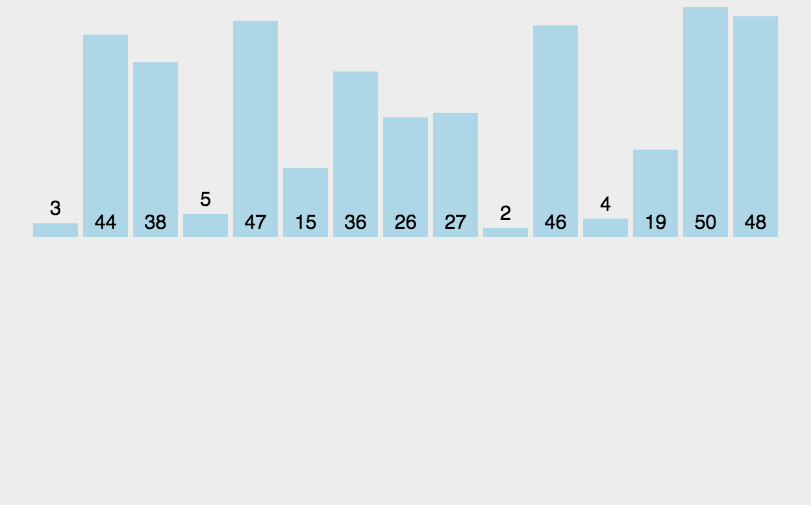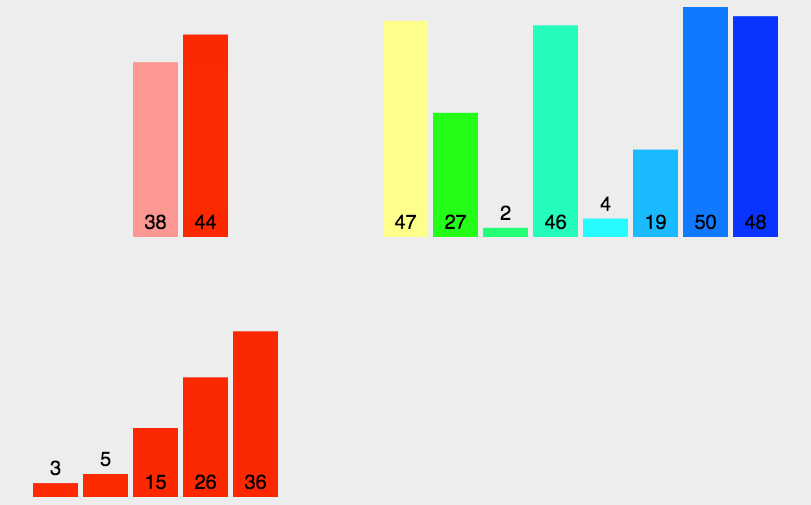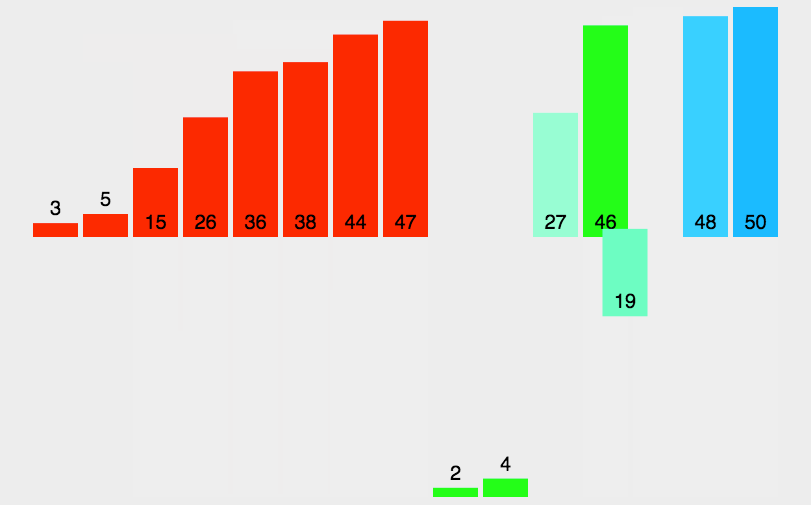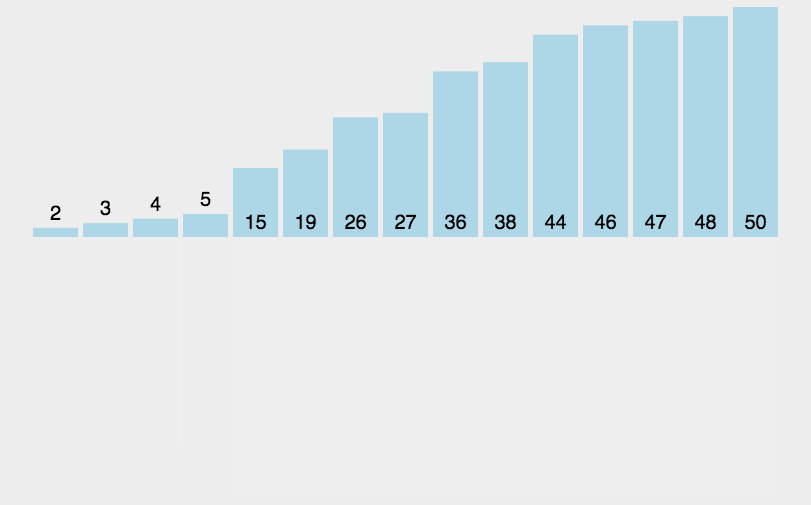
图片解析归并排序

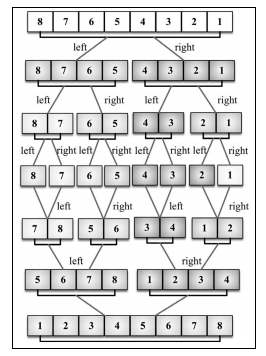
排序思路

由于是分治法，归并排序也是递归的。我们要将算法分为两个函数：

第一个:将一个大数组分为多个小数组并调用用来排序的辅助函数

/**
 * 归并排序
 * 归并排序的基本思想是：将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。
 * @param {array} array 要进行排序的数组
 * @param {function} compareFn // 比较用的方法，默认为defaultCompare
 * @returns {array} 返回排序后的数组
 */
export function mergeSort(array, compareFn = defaultCompare) {
  if (array.length > 1) { // 递归停止条件，当数组的长度为 1时，直接返回，因为它已经排好序了。
    // 如果数组长度比 1 大，那么得将其分成小数组
    const { length } = array; // 声明一个名为length的变量，用来存储数组的长度
    const middle = Math.floor(length / 2); // 首先得找到数组的中间位,找到后我们将数组分成两个小数组,left和right
    /** mergeSort为递归调用自身，直到 left 数组和 right 数组的大小小于等于 1 */
    const left = mergeSort(array.slice(0, middle), compareFn); // left 数组由索引 0 至中间索引的元素组成
    const right = mergeSort(array.slice(middle, length), compareFn); // right 数组由中间索引至原始数组最后一个位置的元素组成
    array = merge(left, right, compareFn); // 获得归并后的数组
  }
  // 返回排序后的数组
  return array;
}

第二个:归并函数，负责合并和排序小数组来产生大数组，直到回到原始数组并已排序完成

/**
 * 归并函数，负责合并和排序小数组来产生大数组，直到回到原始数组并已排序完成
 * @param left 需要合并排序的左侧小数组
 * @param right 需要合并排序的右侧小数组
 * @param compareFn // 传入比较用的方法，默认为defaultCompare
 * @returns {array} 返回两个小数组合并排序后的大数组
 */
function merge(left, right, compareFn) {
  let i = 0; // 用于迭代左侧小数组left的变量
  let j = 0; // 用于迭代右侧小数组right的变量
  const result = []; // 归并结果数组
  while (i < left.length && j < right.length) { // 迭代两个数组
    // 比较来自 left 数组的项是否比来自 right 数组的项小
    // 如果是将该项从 left 数组添加至归并结果数组，并递增用于迭代数组的控制变量
    // 否则，将该项从 right 数组添加项至归并结果数组并递增用于迭代数组的控制变量
    result.push(compareFn(left[i], right[j]) === Compare.LESS_THAN ? left[i++] : right[j++]);
  }
  // 执行完上面的迭代操作，则会有左侧小数组或者右侧小数组已经全部添加到归并结果数组中(可以理解为有一个小数组已经为空)
  // 此时，如果是左侧小数组不为空(i<left.length)，则将 left所有剩余的项添加到归并结果数组中，否则将剩余右侧小数组(right)添加到归并结果数组中
  // 最后，将归并结果数组作为结果返回
  return result.concat(i < left.length ? left.slice(i) : right.slice(j));
}

完整代码实现

// 比较用的常量对象(保证代码优雅)
export const Compare = {
  LESS_THAN: -1, // 如果第一个元素小于第二个元素，它就返回-1
  BIGGER_THAN: 1, // 如果第一个元素大于第二个元素，它就返回1
  EQUALS: 0 // 如果元素有相同的引用，它就返回 0
};
// 比较用的方法
export function defaultCompare(a, b) {
  // 如果元素有相同的引用，它就返回 0
  if (a === b) {
    return Compare.EQUALS;
  }
  // 如果第一个元素小于第二个元素，它就返回-1,否之返回1
  return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
/**
 * 归并函数，负责合并和排序小数组来产生大数组，直到回到原始数组并已排序完成
 * @param left 需要合并排序的左侧小数组
 * @param right 需要合并排序的右侧小数组
 * @param compareFn // 传入比较用的方法，默认为defaultCompare
 * @returns {array} 返回两个小数组合并排序后的大数组
 */
function merge(left, right, compareFn) {
  let i = 0; // 用于迭代左侧小数组left的变量
  let j = 0; // 用于迭代右侧小数组right的变量
  const result = []; // 归并结果数组
  while (i < left.length && j < right.length) { // 迭代两个数组
    // 比较来自 left 数组的项是否比来自 right 数组的项小
    // 如果是将该项从 left 数组添加至归并结果数组，并递增用于迭代数组的控制变量
    // 否则，将该项从 right 数组添加项至归并结果数组并递增用于迭代数组的控制变量
    result.push(compareFn(left[i], right[j]) === Compare.LESS_THAN ? left[i++] : right[j++]);
  }
  // 执行完上面的迭代操作，则会有左侧小数组或者右侧小数组已经全部添加到归并结果数组中(可以理解为有一个小数组已经为空)
  // 此时，如果是左侧小数组不为空(i<left.length)，则将 left所有剩余的项添加到归并结果数组中，否则将剩余右侧小数组(right)添加到归并结果数组中
  // 最后，将归并结果数组作为结果返回
  return result.concat(i < left.length ? left.slice(i) : right.slice(j));
}
/**
 * 归并排序
 * 归并排序的基本思想是：将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。
 * @param {array} array 要进行排序的数组
 * @param {function} compareFn // 比较用的方法，默认为defaultCompare
 * @returns {array} 返回排序后的数组
 */
export function mergeSort(array, compareFn = defaultCompare) {
  if (array.length > 1) { // 递归停止条件，当数组的长度为 1时，直接返回，因为它已经排好序了。
    // 如果数组长度比 1 大，那么得将其分成小数组
    const { length } = array; // 声明一个名为length的变量，用来存储数组的长度
    const middle = Math.floor(length / 2); // 首先得找到数组的中间位,找到后我们将数组分成两个小数组,left和right
    /** mergeSort为递归调用自身，直到 left 数组和 right 数组的大小小于等于 1 */
    const left = mergeSort(array.slice(0, middle), compareFn); // left 数组由索引 0 至中间索引的元素组成
    const right = mergeSort(array.slice(middle, length), compareFn); // right 数组由中间索引至原始数组最后一个位置的元素组成
    array = merge(left, right, compareFn); // 获得归并后的数组
  }
  // 返回排序后的数组
  return array;
}