图的最小生成树算法-Kruskal算法

什么是Kruskal算法

最小生成树是一个图的极小连通子图，它包含原图的所有顶点，并且所有边的权值之和尽可能小。

之前描述了Prim算法是用于生成图结构的最小生成树，而Kruskal算法(中文名:克鲁斯卡尔算法)，是另外一种最小生成树算法，用的也是贪婪算法的思想。

Kruskal算法详细解析

以下算法详细步骤图，均来自B站up主”WAY_zhong”的视频——《最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示》

最小生成树既然是树，则需要遵循树的以下几个规则:

1.因为是树的结构，所有结构中不能形成环。

2.必须连接图结构中的所有顶点，任意两个顶点间都是互通的。

3.如果树有n个顶点，它对应边的个数就是n-1个。

假如有这样一个无向带权图

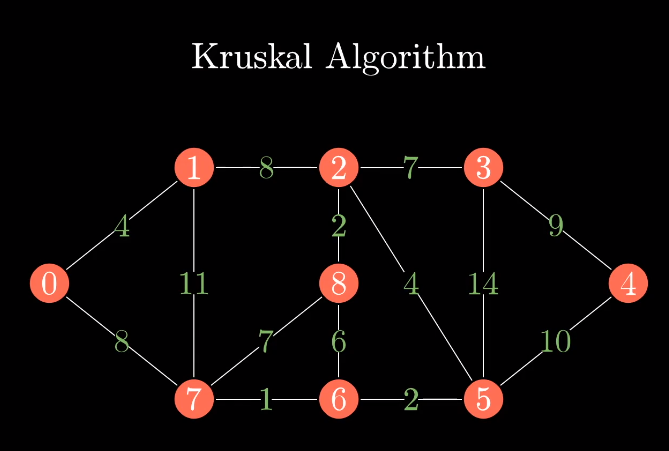
接着把图实例中所有的边取出，放到一个列表中

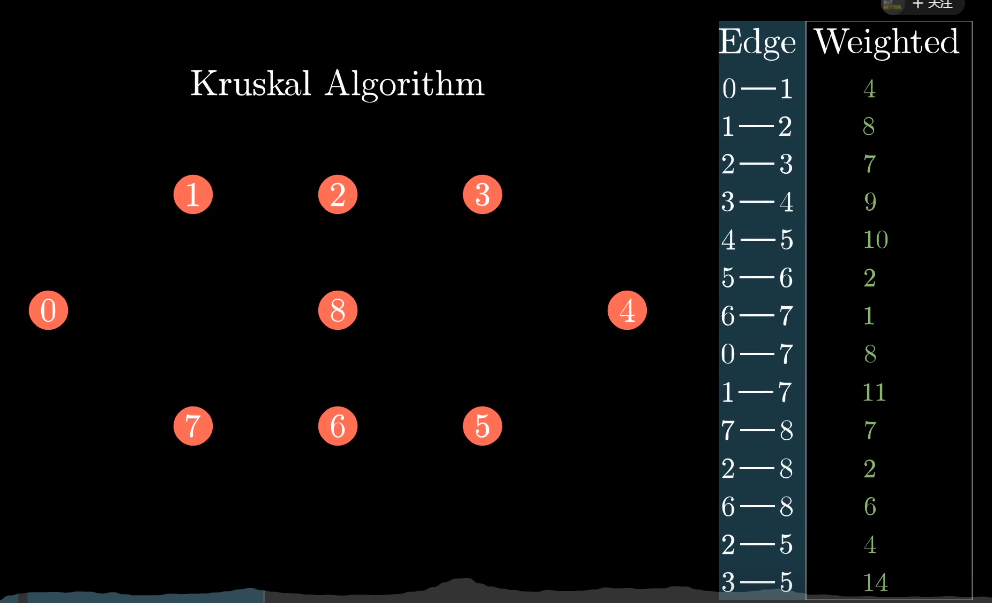
并按照边的权值，由小到大进行排列

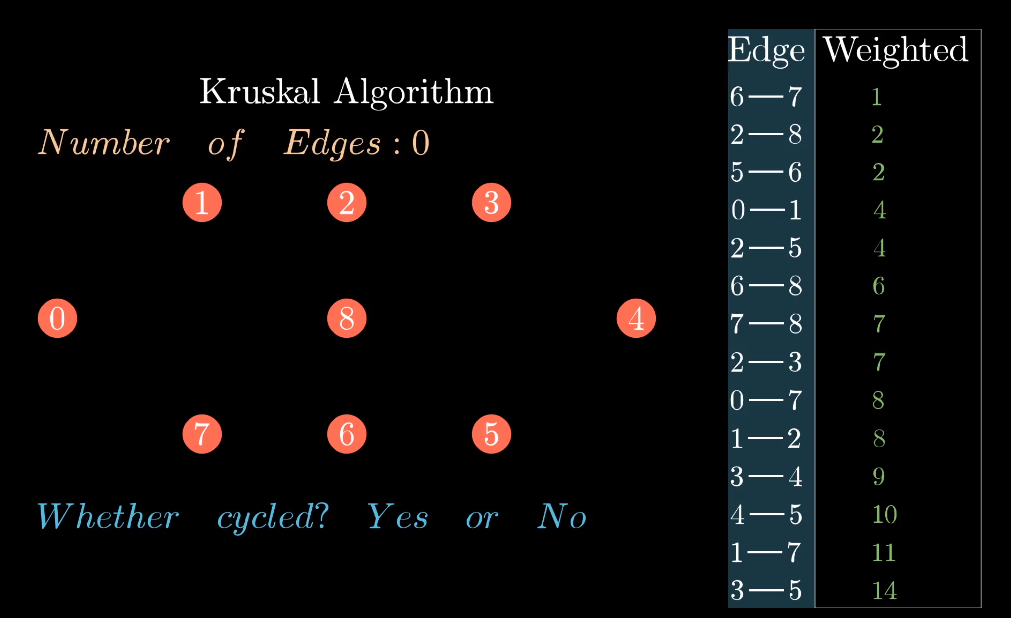
接着在列表中按次序，每次取出一条边，回添到图实例中，不断重复此过程……

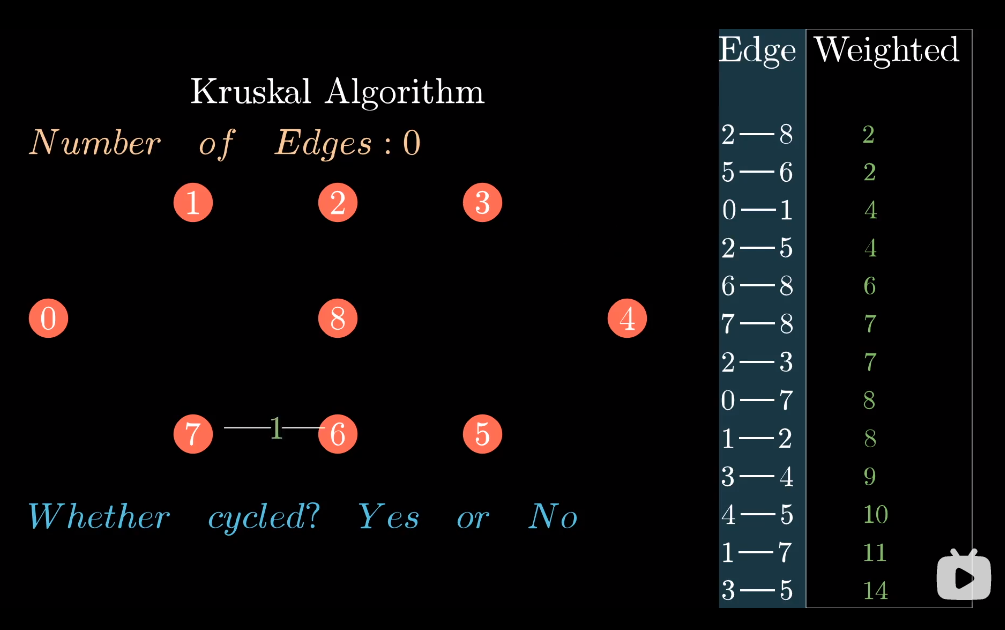
每次添加一条边，都判断是否形成了环(形成了环)，如果如果没有形成环，那么这个条边就会被选中，成为最小生成树的一条边。

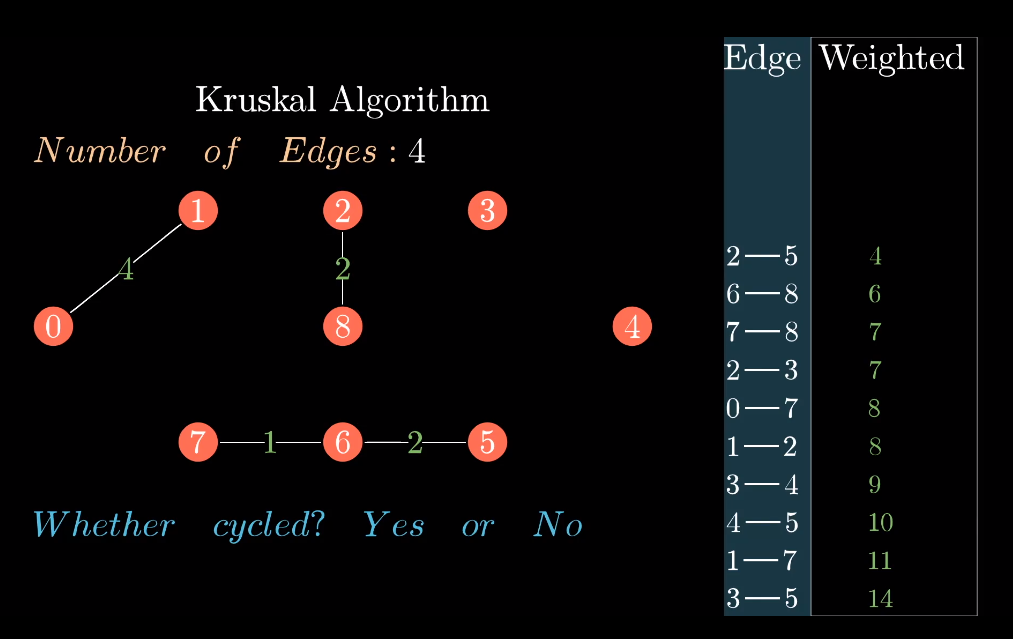
相反，如果形成了环，这条边则会被抛弃，接着判断列表中的下一条边

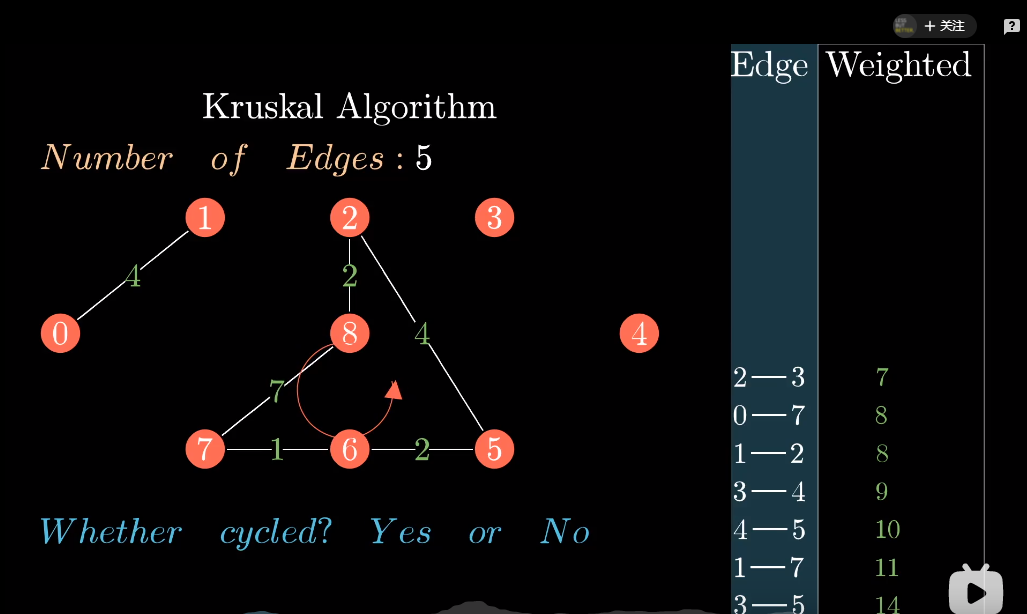
直到选择了n-1条边(满足树对边的规则)，其中n是顶点的个数，此时最小生成树完成。

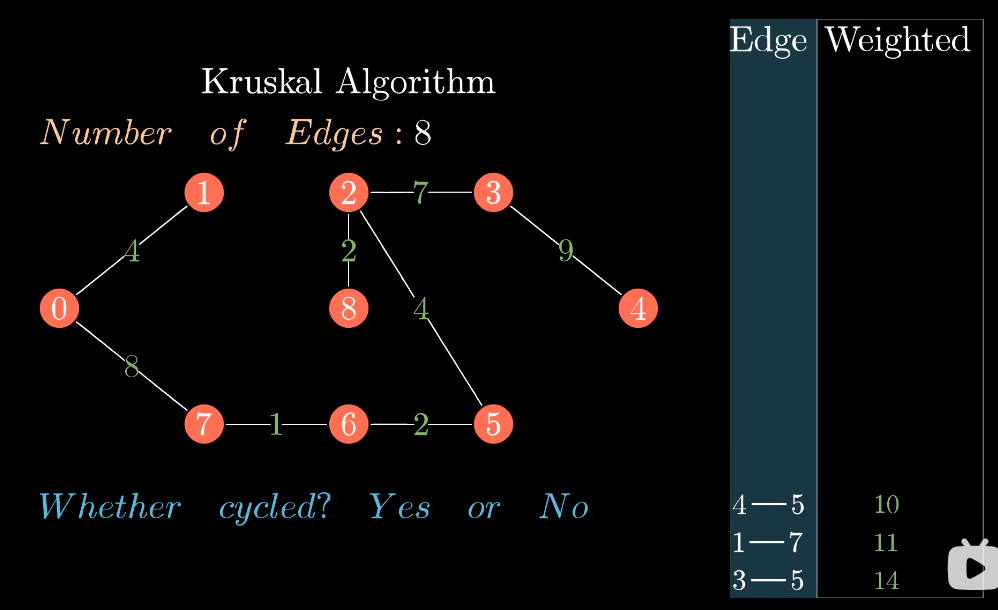
完整可视化算法流程可参考B站原作者的视频:

最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示

代码实现

// INF常量保存Number类型的无穷大
const INF = Number.MAX_SAFE_INTEGER;
/**
 *  检查 MST(最小生成树) 中是否已存在这条边，以避免环路(查找连接顶点的尾部下标)
 * @param {*} i 需要检查的边(连线开始的顶点)
 * @param {*} parent 图实例对应的最小生成树的数组(判断边与边是否形成环路的数组)
 * @returns {*} 返回找到的边
 *  */
const find = (i, parent) => {
  while (parent[i]) { // 如果在最小生成树的数组存在，则把值交给i
    i = parent[i]; // eslint-disable-line prefer-destructuring
  }
  return i; // 将找到的边返回
};
/**
 *  检查 MST(最小生成树) 的边是否相同
 * @param {*} i 需要检查的边i
 * @param {*} j 需要检查的边j
 * @param {*} parent 图实例对应的最小生成树的数组
 * @returns {*} 返回边是否相等，true为不相同，false为相同
 *  */
const union = (i, j, parent) => {
  // 判断两个节点是否在同一颗树中，即是否相交
  if (i !== j) { // 如果i和j是不同的边，说明此边没有与现有生成树形成环路，则将他们加入最小生成树(MST)
    parent[j] = i; // j为父亲节点，i为边权值
    return true;
  }
  return false;
};
/**
 * 对整个图进行拷贝并初始化权值的内部函数
 * @param {*} graph 图实例
 * @returns {*} 返回拷贝且初始化权值后的图实例
 *  */
const initializeCost = graph => {
  const cost = [];
  const { length } = graph;
  for (let i = 0; i < length; i++) {
    cost[i] = [];
    for (let j = 0; j < length; j++) {
      if (graph[i][j] === 0) {
        cost[i][j] = INF;
      } else {
        cost[i][j] = graph[i][j];
      }
    }
  }
  return cost;
};
/**
 * 最小生成树算法-kruskal算法
 * @param {*} graph 需要计算最小生成树的图实例
 * @returns {*} 图实例的最小生成树
 */
export const kruskal = graph => {
  const { length } = graph; //图实例的顶点数量
  const parent = []; //创建最小生成树数组(用一维数组来表达最小生成树，数组下标所对应的元素，代表该顶点在最小生成树当中的父亲节点)
  let ne = 0; // 最小生成树的边数
  let a;
  let b;
  let u;
  let v;
  const cost = initializeCost(graph); // 首先，把邻接矩阵的值复制到 cost 数组，以方便修改且可以保留原始值行
  while (ne < length - 1) { // 当 MST(最小生成树) 的边数小于顶点总数减 1 时(对于有n个顶点的树，它的边是它的顶点总数-1)
    // 找出权值最小的边
    for (let i = 0, min = INF; i < length; i++) { //遍历图的所有顶点，初始化当前最小的权值-min(默认为无穷大)
      for (let j = 0; j < length; j++) { // 遍历当前顶点的邻接矩阵
        if (cost[i][j] < min) { // 如果当前遍历的边权重小于目前记录的最小边(min)
          min = cost[i][j]; // 更新目前记录的最小权值
          a = u = i; // a和u记录当前所存储的最小边的起始顶点
          b = v = j; // b和v记录当前所存储的最小边的到达顶点
        }
      }
    }
    u = find(u, parent); // 通过下标(也就是父亲节点)检查 MST(最小生成树) 中是否已存在这条边，以避免环路
    v = find(v, parent); // 通过下标(也就是父亲节点)检查 MST(最小生成树) 中是否已存在这条边，以避免环路
    if (union(u, v, parent)) { // 如果 u 和 v 是不同的边(不同的父亲节点，没有形成环路)，则将其加入 MST(最小生成树) 
      ne++; // 最小生成树的边数
    }
    cost[a][b] = cost[b][a] = INF; // 从列表中移除这些边，以免重复计算
  }
  // 返回MST(最小生成树)
  return parent;
};