什么是最小生成树

最小生成树是一个图的极小连通子图，它包含原图的所有顶点，并且所有边的权值之和尽可能小。

Prim算法就是图的最小生成树算法之一，Prim 算法是一种求解加权无向连通图的 MST 问题的贪心算法。它能找出一个边的子集，使得其构成的树包含图中所有顶点，且边的权值之和最小。

Prim算法以图的顶点为基础，从首个初始顶点，寻找到达其他顶点权值最小的边，并把该顶点加入到“已到达顶点”的集合中，此时，这个集合就是这个图的最小生成树。

一般用一维数组比较方便表达最小生成树，数组下标所对应的元素，代表该顶点在最小生成树当中的父亲节点。

假设有这样一个带权图:

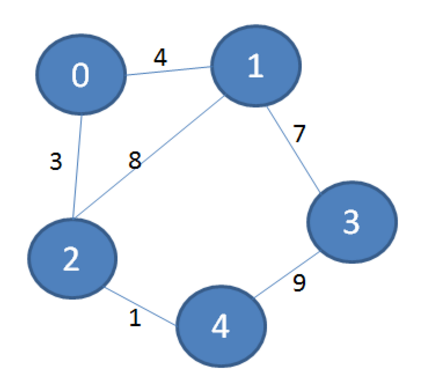
它所有权值最小的边形成的集合如下:

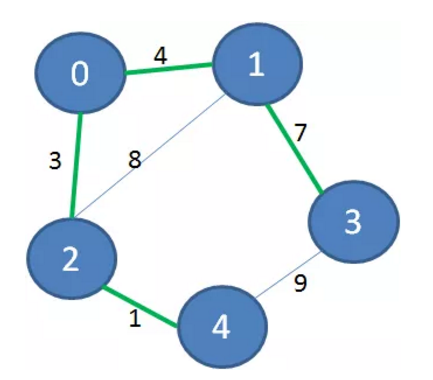
去掉多余的边，就是该图实例的最小生成树:

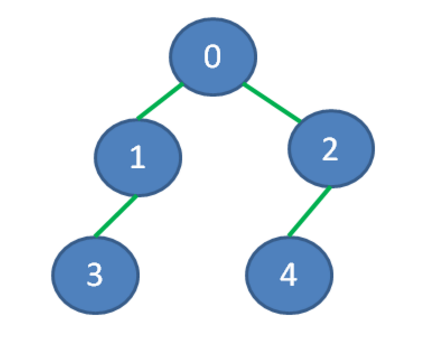
Prim算法详细步骤

以下算法详细步骤图，均来自公众号”程序员小灰”的文章——《漫画：什么是最小生成树？》

以图的第一个顶点作为初始顶点，加入到“已到达顶点”的集合中。

第一个顶点总是MST(最小生成树)的根节点，但是因为根节点没有父亲节点，所以根节点的元素值是-1。

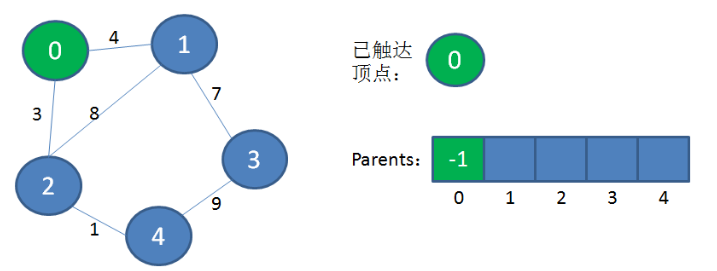
此时从“已到达顶点”的集合出发，发现0到2的权值最小，把顶点2加入到“已到达顶点”的集合中，因为它的父亲节点是根节点，所以它的元素值是0。

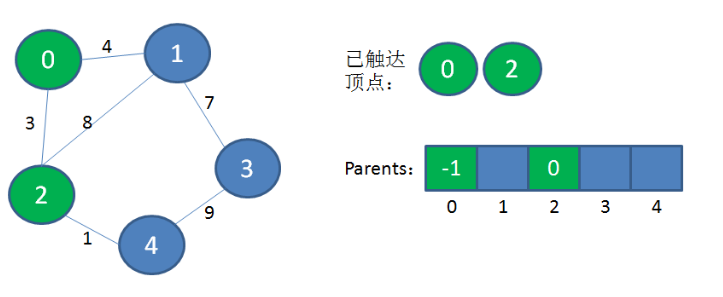
继续从“已到达顶点”的集合出发，发现2到4的权值最小，把顶点4加入到“已到达顶点”的集合中，因为它的父亲节点是2，所以它的元素值是2。

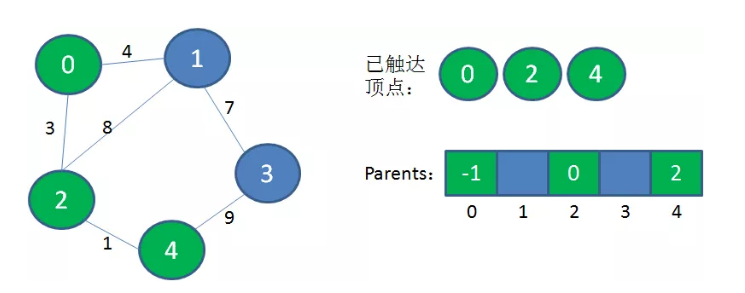
继续从“已到达顶点”的集合出发，发现0到1的权值最小，把顶点1加入到“已到达顶点”的集合中，因为它的父亲节点是0，所以它的元素值是0。

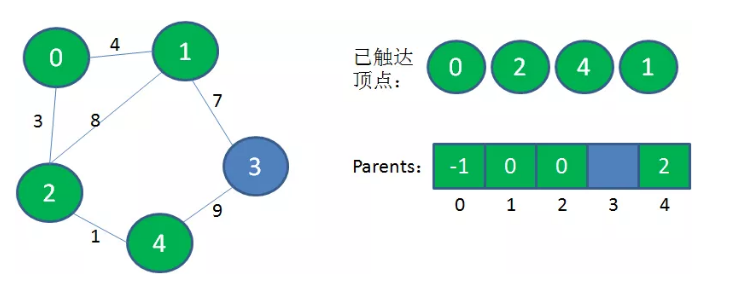
继续从“已到达顶点”的集合出发，发现1到3的权值最小，把顶点3加入到“已到达顶点”的集合中，因为它的父亲节点是1，所以它的元素值是1。

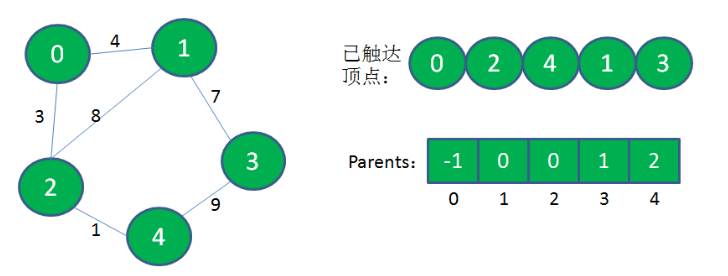
此时，“已到达顶点”的集合，就是这个带权图的最小生成树。

Prim算法代码实现

如果仔细观察，可以发现Prim算法和Dijkstra算法特别相似，只有少部分代码有不同。

// INF常量保存Number类型的无穷大
const INF = Number.MAX_SAFE_INTEGER;
/**
 * 寻找未处理顶点集合中挑选出权值最小的顶点的内部函数
 * @param {*} graph 需要计算最小生成树的图实例
 * @param {*} key 图实例的顶点权值表
 * @param {*} visited 图实例的访问记录表
 * @returns {*} 返回图实例中所有未处理顶点中权值最小的顶点
 *  */
const minKey = (graph, key, visited) => {
  // Initialize min value
  let min = INF; // 初始化当前最小的权值(默认为无穷大)
  let minIndex = 0; // 存储当前权值最小顶点的下标
  for (let v = 0; v < graph.length; v++) { // 遍历图实例的顶点列表
    if (visited[v] === false && key[v] < min) { // 如果该顶点没有访问过，且该顶点的权值小于目前的最小权值(min)
      min = key[v]; // 更新当前最小的权值
      minIndex = v; // 更新当前权值最小顶点的下标
    }
  }
  // 找到图实例中所有未处理顶点中权值最小的顶点，将其返回
  return minIndex; // 返回图实例中所有未处理顶点中权值最小的顶点
};
/**
 * 最小生成树算法-Prim算法
 * @param {*} graph 需要计算最小生成树的图实例
 * @returns {*} 图实例的最小生成树
 */
export const prim = graph => {
  const parent = []; //创建最小生成树数组(用一维数组来表达最小生成树，数组下标所对应的元素，代表该顶点在最小生成树当中的父亲节点)
  const key = []; //创建记录顶点权值的数组
  const visited = []; //创建顶点的触达记录表，记录遍历触达过的顶点
  const { length } = graph; //图实例的顶点数量
  //初始化顶点权值数组，把所有顶点初始化为正无穷(INF)
  // 初始化访问记录表，每个顶点的访问记录均为未访问(false)
  for (let i = 0; i < length; i++) {
    key[i] = INF;
    visited[i] = false;
  }
  key[0] = 0; // 选择第一个key作为第一个顶点
  parent[0] = -1; // 第一个顶点总是MST(最小生成树)的根节点，但是因为根节点没有父亲节点，所以根节点的元素值是-1，因此parent[0]= -1
  //主循环，遍历图实例所有顶点,寻找未处理顶点集合中权值最小的顶点
  for (let i = 0; i < length - 1; i++) {
    const u = minKey(graph, key, visited); // 从未处理的顶点集合中选出权值(key值)最小的顶点，传入graph(图实例)，key(图实例顶点权值数组)和visited(图实例的访问记录表)
    visited[u] = true; // 将当前顶点加入已触达顶点
    for (let v = 0; v < length; v++) { // 遍历顶点(也就是遍历当前顶点的邻接矩阵)
      if (graph[u][v] && !visited[v] && graph[u][v] < key[v]) { // 如果得到更小的权值(顶点的权值存在，且未触达过，且当前领接矩阵点的权值小于当前记录的权值)
        parent[v] = u; //则保存到最小生成树(MST)路径(parent)
        key[v] = graph[u][v]; // 并更新其权值
      }
    }
  }
  return parent; // 处理完所有顶点后，返回包含最小生成树(MST)的结果
};

代码实例

如果对以下的图执行Prim算法:

let graph = [
 [0, 2, 4, 0, 0, 0],
 [2, 0, 2, 4, 2, 0],
 [4, 2, 0, 0, 3, 0],
 [0, 4, 0, 0, 3, 2],
 [0, 2, 3, 3, 0, 2],
 [0, 0, 0, 2, 2, 0]
]; 

可以得到如下输出结果

/**
Edge   Weight
0 - 1  2
1 - 2  2
5 - 3  2
1 - 4  2
4 - 5  2 
**/