深度优先搜索

什么是深度优先搜索(DFS)

前一篇描述了，搜索图的算法之一的广度优先搜索（breadth-first search，BFS），而另外一种搜索图的算法，则是深度优先搜索（depth-first search，DFS）。

深度优先搜索算法(DFS)会从第一个指定的顶点开始遍历图，沿着路径直到这条路径的最后一个顶点被访问了，再原路折回探索吓一跳路径。

深度优先搜索是”先深度后广度地访问顶点”的图搜索算法。

深度优先搜索(DFS)全过程

例如用下面的图结构，从顶点A开始搜索，直到搜索到顶点G。

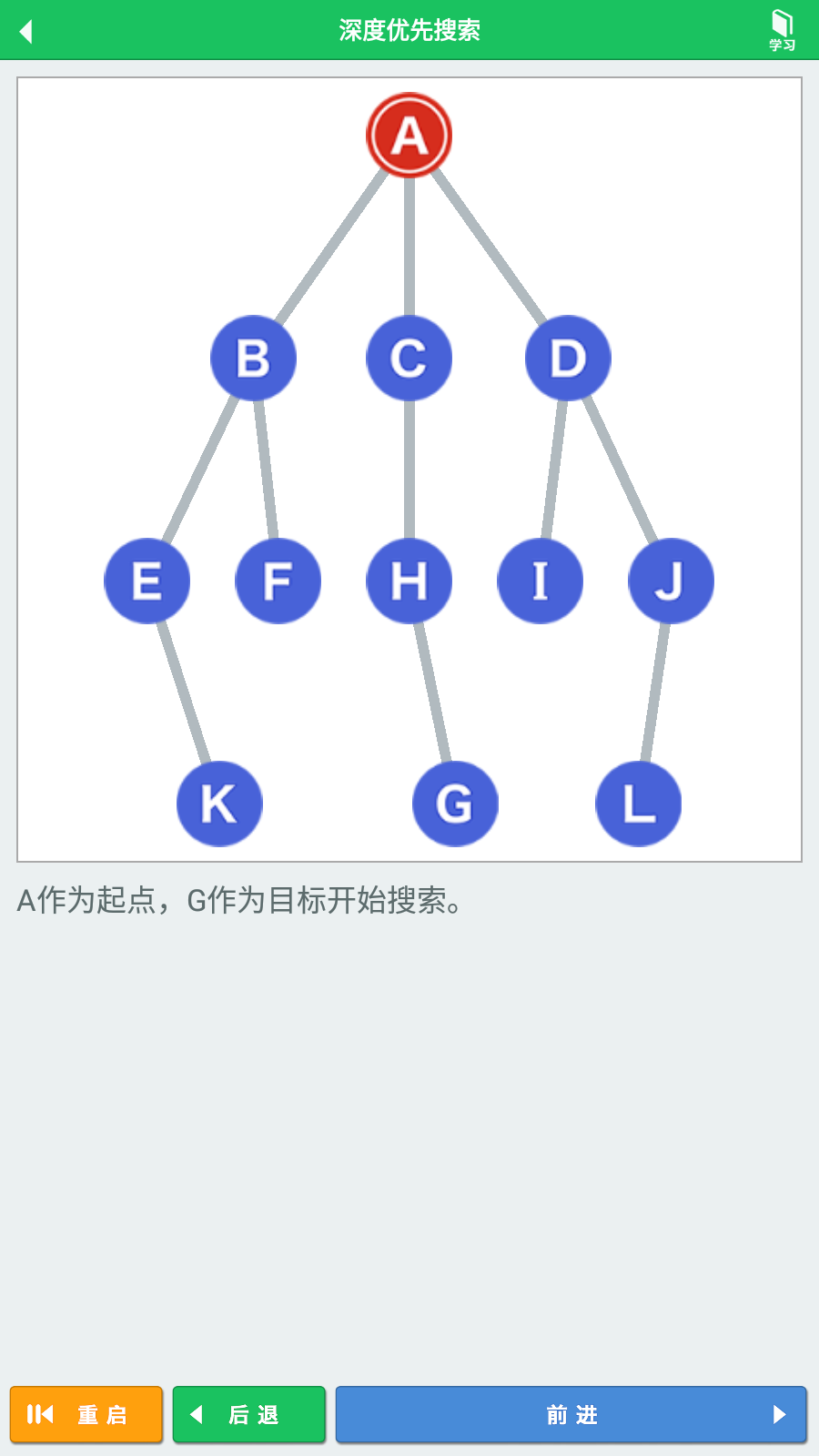
深度优先搜索-图解过程1

可以知道，顶点A的相邻顶点有顶点B、顶点C、顶点D，这三个顶点，将它们视为下一步的候选顶点，按顺序逐个深度递归搜索。由于顶点B是最先探索到的相邻顶点，则从顶点B开始深度探索，移动到顶点B。

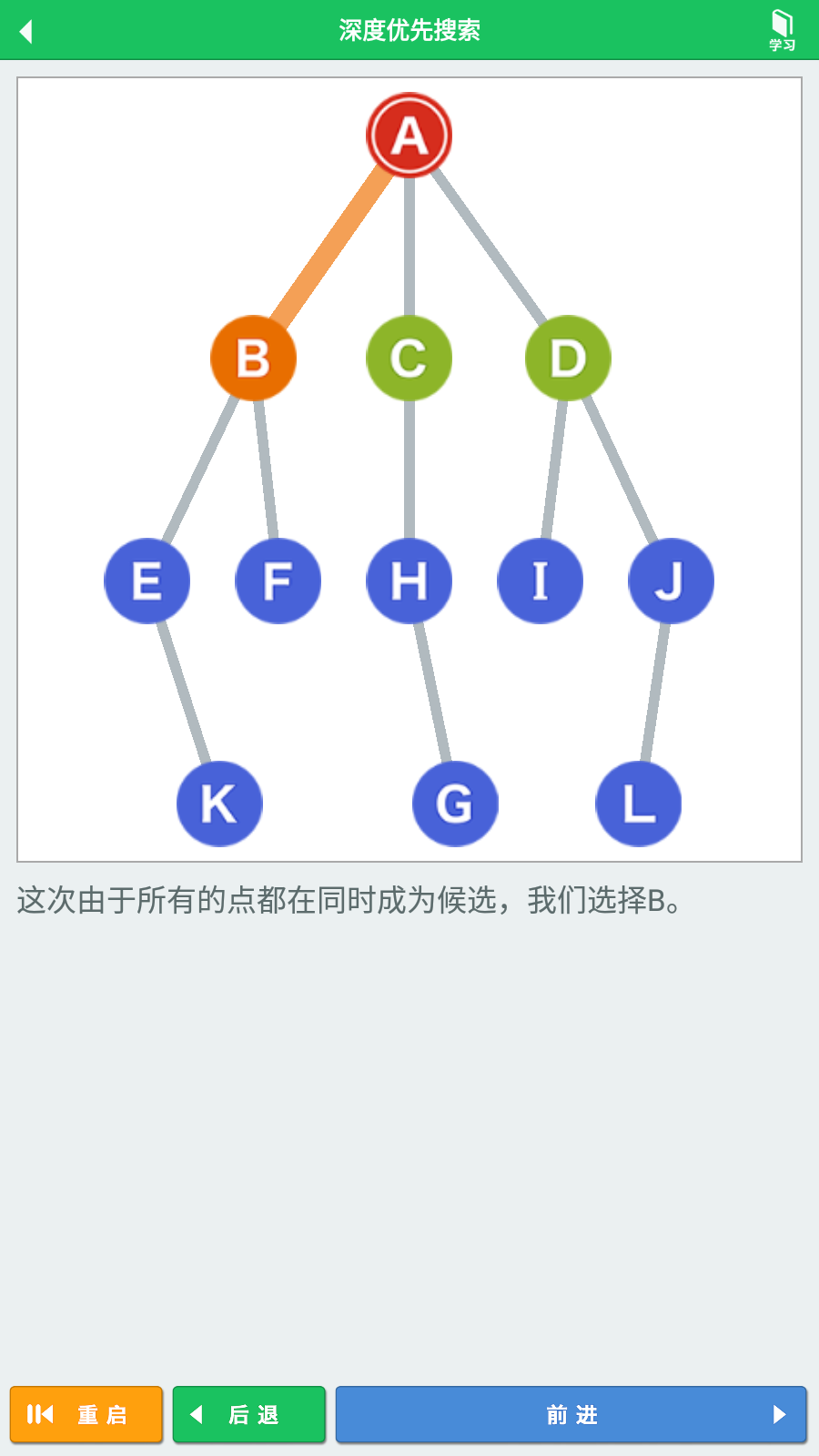
深度优先搜索-图解过程2

到达顶点B，可以获知它的相邻顶点是E和F，则将它们视为下一步的候选顶点，由于顶点E是最先探索到的相邻顶点，则继续从顶点E开始深度探索，移动到顶点E。

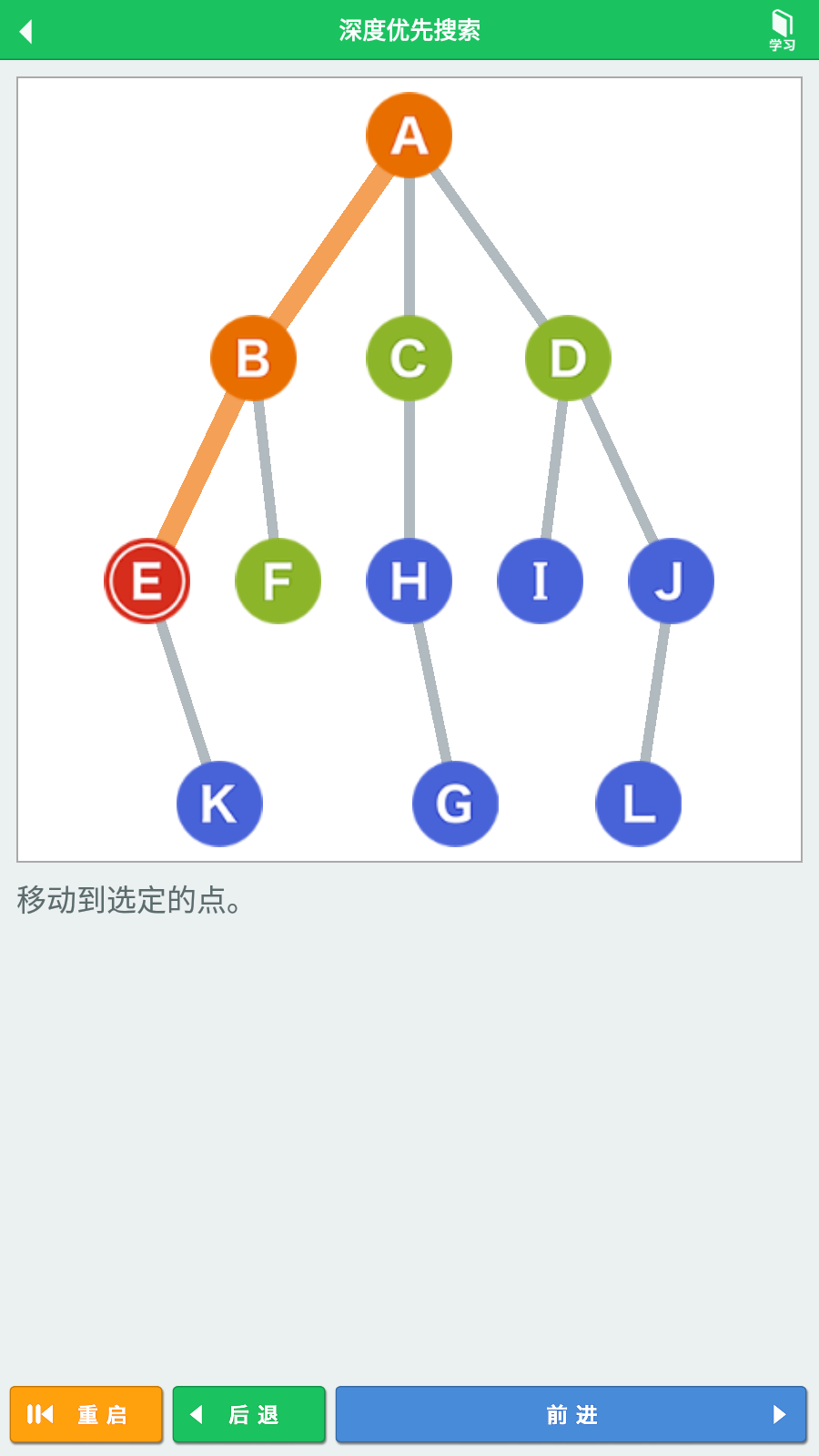
深度优先搜索-图解过程3

到达顶点E，可以获知它的相邻顶点是K，则将它视为下一步的候选顶点，继续从顶点K开始深度探索，移动到顶点K。

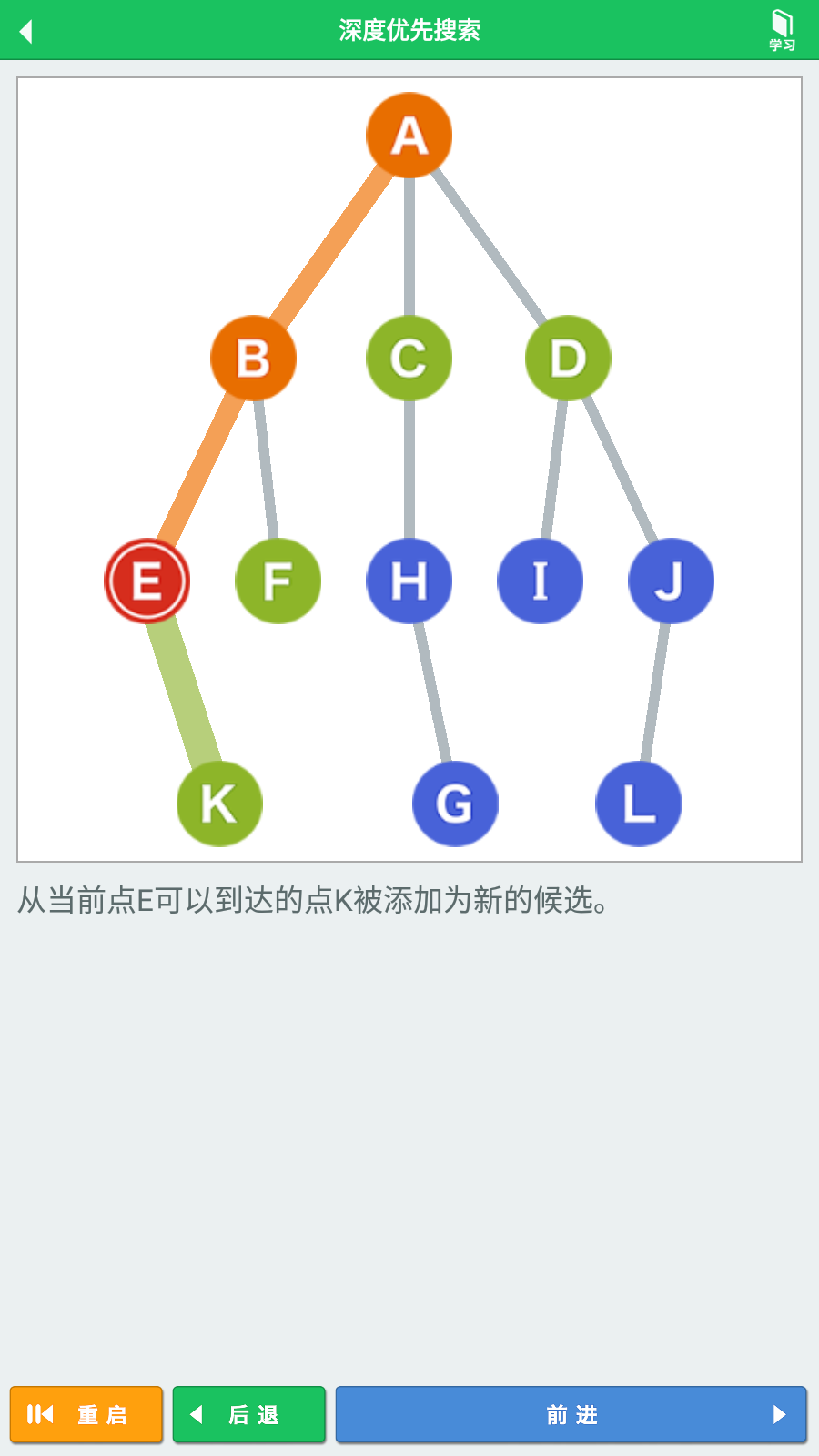
深度优先搜索-图解过程4

到达顶点K，由于顶点K没有路径下的相邻顶点，则原路折返知道有未探索顶点的顶点B，探索顶点F。

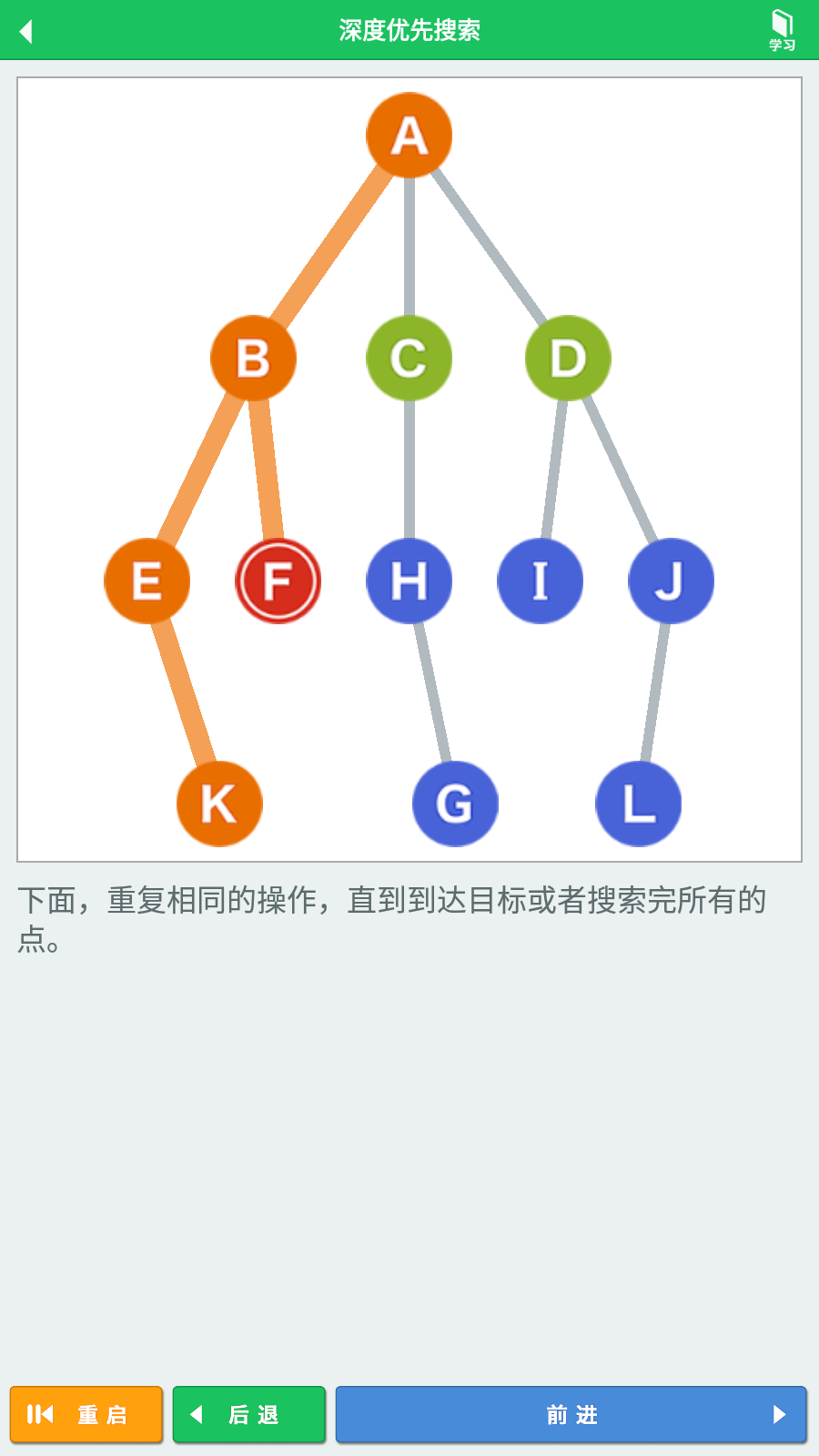
深度优先搜索-图解过程5

接下来不断重复相同的操作:

到达顶点F，由于顶点F没有路径下的相邻顶点，则原路折返知道有未探索顶点的顶点A，探索顶点C。
到达顶点C，可以获知它的相邻顶点是H，则将它视为下一步的候选顶点，继续从顶点H开始深度探索，移动到顶点H。
到达顶点C，可以获知它的相邻顶点是H，则将它视为下一步的候选顶点，继续从顶点H开始深度探索，移动到顶点H。
到达顶点H，可以获知它的相邻顶点是G，则将它视为下一步的候选顶点，继续从顶点G开始深度探索，移动到顶点G。
到达顶点G，找到需要到达的目标，结束搜索。

实现深度优先搜索(DFS)

代码流程

为了标记图的顶点，我们需要提供一个表示顶点颜色的常量对象。
- 白色(WHITE):表示该顶点还没有被访问
- 灰色(GREY):表示该顶点被访问过，但并未被探索过
- 黑色(BLACK):表示该顶点被访问过且被完全探索过

// 广度优先算法中标记顶点的常量对象
const Colors = {
  WHITE: 0, // 表示该顶点还没有被访问
  GREY: 1, // 表示该顶点被访问过，但并未被探索过
  BLACK: 2 // 表示该顶点被访问过且被完全探索过
};

并且提供一个辅助方法，用于初始化每个顶点颜色。

/**
 * 辅助方法:初始化每个顶点的颜色的函数
 * @param {*} vertices 顶点列表
 * @returns {*} 返回初始化顶点颜色后的对象
 */
const initializeColor = vertices => {
  const color = {};
  for (let i = 0; i < vertices.length; i++) {
    color[vertices[i]] = Colors.WHITE;
  }
  return color;
};

接着便是深度优先搜索算法的完整代码思路:

声明广度优先搜索算法的函数-depthFirstSearch，接收两个参数，分别是graph(要遍历的图实例)和callback(回调函数)
在函数内获取传入图实例(graph)的顶点列表、邻接表，并将图的顶点列表中的所有顶点初始化颜色为白色(表示该顶点还没有被访问)
遍历图实例的所有顶点，如果当前遍历的顶点项是白色(表示该顶点还没有被访问)，则递归访问这个顶点,递归顶点使用的函数-depthFirstSearchVisit，传入函数需要的四个参数要访问的顶点(u)、图所有顶点的颜色对象(color)、图的邻接表(adjList)和回调函数(callback)，它内部的代码流程:
- 把当前访问的顶点项(u)，标识为灰色(该顶点被访问过，但并未被探索过)
- 如果有传入回调函数，则执行该回调函数，回调函数会将这个顶点作为入参方法。(执行该函数输出已访问过的顶点)
- 获取当前访问顶点项(u)的邻接表，如果这个顶点的邻接表不为空，则遍历这个顶点的邻接表中的顶点，遍历时，如果该邻接表的顶点是白色，则以该邻接表的顶点，进行递归访问。
这个顶点的邻接表探索完后，将这个顶点标识为黑色(已被访问且被完全探索)

代码实现

/**
 * 深度优先搜索顶点(私有函数)
 * @param {*} u 要访问的顶点
 * @param {object} color 图所有顶点的颜色对象
 * @param {*} adjList 图的邻接表
 * @param {function} callback 回调函数
 */
const depthFirstSearchVisit = (u, color, adjList, callback) => {
  color[u] = Colors.GREY; // 当前访问的顶点u标识为灰色(该顶点被访问过，但并未被探索过)
  // 如果存在回调函数
  if (callback) {
    callback(u); // 则指向回调函数，入参顶点u(执行该函数输出已访问过的顶点)
  }
  // console.log('Discovered ' + u);
  const neighbors = adjList.get(u); // 获取顶点u的邻接表
  for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表
    const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w
    if (color[w] === Colors.WHITE) { // 如果当前顶点w是白色(顶点还没有被访问),则以w为顶点进行递归访问
      depthFirstSearchVisit(w, color, adjList, callback);
    }
  }
  color[u] = Colors.BLACK; // 最后标识u为黑色(该顶点被访问过且被完全探索过)
  // console.log('explored ' + u);
};

/**
 * 图的深度优先搜索算法
 * 使用到的数据结构:堆栈
 * 概念:先深度后广度地访问顶点
 * @param {*} graph 要进行遍历的图
 * @param {function} callback 回调函数
 */
export const depthFirstSearch = (graph, callback) => {
  const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表
  const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表
  const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色

  for (let i = 0; i < vertices.length; i++) { // 遍历图的所有顶点
    if (color[vertices[i]] === Colors.WHITE) { // 如果当前顶点为白色(该顶点还没有被访问)
      depthFirstSearchVisit(vertices[i], color, adjList, callback); // 则调用私有的递归函数搜索顶点
    }
  }
};

代码用例

我们初始化一个图，用于测试深度优先搜索。

let graph = new Graph();
const myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
for (let i = 0; i < myVertices.length; i++) {
  graph.addVertex(myVertices[i]);
}
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("C", "D");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("E", "I");

// 将这个实例图，用广度优先搜索算法打印出来。

const printVertex = (value) => console.log('Visited vertex: ' + value);
depthFirstSearch(graph, printVertex);

/**
 *
Visited vertex: A
Visited vertex: B
Visited vertex: E
Visited vertex: I
Visited vertex: F
Visited vertex: C
Visited vertex: D
Visited vertex: G
Visited vertex: H 
*/

深度优先搜索算法(DFS)还可以做更多

深度优先搜索算法的工作原理了解之后，它还可以做更多事情，比如使用它来搜索图顶点的初次发现时间、完成访问时间，或者图中某个顶点的前溯点。

下面是一段利用DFS探索图实例中每个顶点的初次发现时间、完成访问时间和前溯点。

代码实现

/**
 * 深度探索顶点
 * @param u 要访问的顶点
 * @param color 颜色对象
 * @param d 图中每个顶点的初次发现时间
 * @param f 图中每个顶点的完成访问时间
 * @param p 图中每个顶点的前溯点
 * @param time 初始时间
 * @param adjList 图的临接表
 * @constructor
 */
const DFSVisit = (u, color, d, f, p, time, adjList) => {
  // console.log('discovered ' + u);
  color[u] = Colors.GREY; // 当前访问的顶点u标识为灰色(该顶点被访问过，但并未被探索过)
  d[u] = ++time.count; // 递增(追加)当前顶点的发现时间
  const neighbors = adjList.get(u); // 获取顶点u的邻接表
  for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表
    const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w
    if (color[w] === Colors.WHITE) { // 如果当前顶点w是白色(顶点还没有被访问),则以w为顶点进行递归访问
      p[w] = u; // 当顶点w是由引自顶点u的边而被发现的，设置顶点w的前溯点为顶点u
      DFSVisit(w, color, d, f, p, time, adjList); // 以w为顶点进行递归访问
    }
  }
  color[u] = Colors.BLACK; // 最后标识u为黑色(该顶点被访问过且被完全探索过)
  f[u] = ++time.count; //递增(追加)顶点u的发现时间，并记录在顶点u的完成访问时间中
  // console.log('explored ' + u);
};

/**
 * 使用深度优先算法探索图
 * @param {*} graph 要进行搜索的图(Graph 类实例)
 */
export const DFS = graph => {
  const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表
  const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表
  const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色
  const d = {}; // 存储每个顶点的发现时间(distances)
  const f = {}; // 存储每个顶点完成访问的时间(distances)
  const p = {}; // 存储前溯点(predecessors)
  const time = {
    count: 0
  }; // time来追踪发现时间和完成探索时间
  for (let i = 0; i < vertices.length; i++) { // 遍历图的顶点列表，完成初始化
    f[vertices[i]] = 0; // 初始化图中每一个顶点的完成访问时间为0
    d[vertices[i]] = 0; // 初始化图中每一个顶点的发现时间为0
    p[vertices[i]] = null; // 初始化图中每一个顶点的前溯点为null
  }
  for (let i = 0; i < vertices.length; i++) { // 再次遍历图的顶点列表，完成初始化
    if (color[vertices[i]] === Colors.WHITE) { // 如果遍历的当前项顶点是白色(该顶点还没有被访问)
      DFSVisit(vertices[i], color, d, f, p, time, adjList); // 则调用私有的递归函数深度探索顶点
    }
  }
  // 最后，返回distances对象、finished对象和predecessors对象
  return {
    discovery: d,
    finished: f,
    predecessors: p
  };
};

使用DFS实现拓扑排序

什么是拓扑排序

当我需要编排一些任务或步骤的执行顺序时，这称为拓扑排序（topological sorting，英文亦写作 topsort 或是 toposort）。

例如，当开始学习一门计算机科学课程，在学习某些知识之前得按顺序完成一些知识储备（你不可以在上算法 I 课程前先上算法 II 课程）。

当我们在开发一个项目时，需要按顺序执行一些步骤。例如，首先从客户那里得到需求，接着开发客户要求的东西，最后交付项目。你不能先交付项目再去收集需求。

代码用例

/**
 * 使用DFS实现拓扑排序
 */

graph = new Graph(true); // 有向图
myVertices = ['A', 'B', 'C', 'D', 'E', 'F'];
for (i = 0; i < myVertices.length; i++) {
  graph.addVertex(myVertices[i]);
}
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('B', 'D');
graph.addEdge('B', 'E');
graph.addEdge('C', 'F');
graph.addEdge('F', 'E');
const result = DFS(graph);

/**
distances: { A:1, B:11, C:2, D:8, E:4, F:3 }
finished: { A:10, B: 12, C:7, D:9, E:5, F:6 }
predecessors: [A: null, B: null, C: "A", D: "A", E: "B", F: "C"]
顶点A的发现时间为1,完成访问时间是10，前溯点为null
顶点B的发现时间为11，完成访问时间是12，前溯点为null
顶点C的发现时间为2，完成访问时间是7，前溯点为A
顶点D的发现时间为8，完成访问时间是9，前溯点为A
顶点E的发现时间为4，完成访问时间是5，前溯点为B
顶点F的发现时间为3，完成访问时间是6，前溯点为C
  */

const fTimes = result.finished; // 图的每个顶点的完成访问的时间
let s = ''; // 用于输出排序的字符串
for (let count = 0; count < myVertices.length; count++) { // 遍历图的顶点列表
  let max = 0; // 初始化max变量存储最大的顶点完成访问时间
  let maxName = null; // 初始化maxName变量存储完成访问时间最大的顶点
  for (i = 0; i < myVertices.length; i++) { // 再次遍历图的顶点列表
    if (fTimes[myVertices[i]] > max) { // 如果当前顶点的完成访问时间大于max
      max = fTimes[myVertices[i]]; // 设置max为当前顶点的完成访问时间
      maxName = myVertices[i]; // 设置maxName为当前顶点
    }
  }
  s += ' - ' + maxName; // 向字符串追加顶点
  delete fTimes[maxName]; // 从图的完成访问时间对象中删除当前顶点
}
console.log(s);
 /**
  * 最终输出结果(依据图顶点的完成访问时间大小倒序排列)
  * B - A - D - C - F - E
  */

完整代码实现

附上上述所有代码的完整实现

import {
  Queue
} from '/Queue/app.js';
import {
  Graph
} from '/Graph/app.js';

/**
 * 有两种算法可以对图进行遍历：广度优先搜索（breadth-first search，BFS）和深度优先搜索（depth-first search，DFS）。图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环，等等。
 */

// 深度优先算法中标记顶点的常量对象
const Colors = {
  WHITE: 0, // 表示该顶点还没有被访问
  GREY: 1, // 表示该顶点被访问过，但并未被探索过
  BLACK: 2 // 表示该顶点被访问过且被完全探索过
};
/**
 * 辅助方法:初始化每个顶点的颜色的函数
 * @param {*} vertices 顶点列表
 * @returns {*} 返回初始化顶点颜色后的对象
 */
const initializeColor = vertices => {
  const color = {};
  for (let i = 0; i < vertices.length; i++) {
    color[vertices[i]] = Colors.WHITE;
  }
  return color;
};
/**
 * 深度优先搜索顶点(私有函数)
 * @param {*} u 要访问的顶点
 * @param {object} color 图所有顶点的颜色对象
 * @param {*} adjList 图的邻接表
 * @param {function} callback 回调函数
 */
const depthFirstSearchVisit = (u, color, adjList, callback) => {
  color[u] = Colors.GREY; // 当前访问的顶点u标识为灰色(该顶点被访问过，但并未被探索过)
  // 如果存在回调函数
  if (callback) {
    callback(u); // 则指向回调函数，入参顶点u(执行该函数输出已访问过的顶点)
  }
  // console.log('Discovered ' + u);
  const neighbors = adjList.get(u); // 获取顶点u的邻接表
  for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表
    const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w
    if (color[w] === Colors.WHITE) { // 如果当前顶点w是白色(顶点还没有被访问),则以w为顶点进行递归访问
      depthFirstSearchVisit(w, color, adjList, callback);
    }
  }
  color[u] = Colors.BLACK; // 最后标识u为黑色(该顶点被访问过且被完全探索过)
  // console.log('explored ' + u);
};

/**
 * 图的深度优先搜索算法
 * 使用到的数据结构:堆栈
 * 概念:先深度后广度地访问顶点
 * @param {*} graph 要进行遍历的图
 * @param {function} callback 回调函数
 */
export const depthFirstSearch = (graph, callback) => {
  const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表
  const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表
  const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色

  for (let i = 0; i < vertices.length; i++) { // 遍历图的所有顶点
    if (color[vertices[i]] === Colors.WHITE) { // 如果当前顶点为白色(该顶点还没有被访问)
      depthFirstSearchVisit(vertices[i], color, adjList, callback); // 则调用私有的递归函数搜索顶点
    }
  }
};

let graph = new Graph();
const myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
for (let i = 0; i < myVertices.length; i++) {
  graph.addVertex(myVertices[i]);
}
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("C", "D");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("E", "I");

// 将这个实例图，用广度优先搜索算法打印出来。

const printVertex = (value) => console.log('Visited vertex: ' + value);
depthFirstSearch(graph, printVertex);

/**
 *
Visited vertex: A
Visited vertex: B
Visited vertex: E
Visited vertex: I
Visited vertex: F
Visited vertex: C
Visited vertex: D
Visited vertex: G
Visited vertex: H 
*/


/**
 * 深度探索顶点
 * @param u 要访问的顶点
 * @param color 颜色对象
 * @param d 图中每个顶点的初次发现时间
 * @param f 图中每个顶点的完成访问时间
 * @param p 图中每个顶点的前溯点
 * @param time 初始时间
 * @param adjList 图的临接表
 * @constructor
 */
const DFSVisit = (u, color, d, f, p, time, adjList) => {
  // console.log('discovered ' + u);
  color[u] = Colors.GREY; // 当前访问的顶点u标识为灰色(该顶点被访问过，但并未被探索过)
  d[u] = ++time.count; // 递增(追加)当前顶点的发现时间
  const neighbors = adjList.get(u); // 获取顶点u的邻接表
  for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表
    const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w
    if (color[w] === Colors.WHITE) { // 如果当前顶点w是白色(顶点还没有被访问),则以w为顶点进行递归访问
      p[w] = u; // 当顶点w是由引自顶点u的边而被发现的，设置顶点w的前溯点为顶点u
      DFSVisit(w, color, d, f, p, time, adjList); // 以w为顶点进行递归访问
    }
  }
  color[u] = Colors.BLACK; // 最后标识u为黑色(该顶点被访问过且被完全探索过)
  f[u] = ++time.count; //递增(追加)顶点u的发现时间，并记录在顶点u的完成访问时间中
  // console.log('explored ' + u);
};

/**
 * 使用深度优先算法探索图
 * @param {*} graph 要进行搜索的图(Graph 类实例)
 */
export const DFS = graph => {
  const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表
  const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表
  const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色
  const d = {}; // 存储每个顶点的发现时间(distances)
  const f = {}; // 存储每个顶点完成访问的时间(distances)
  const p = {}; // 存储前溯点(predecessors)
  const time = {
    count: 0
  }; // time来追踪发现时间和完成探索时间
  for (let i = 0; i < vertices.length; i++) { // 遍历图的顶点列表，完成初始化
    f[vertices[i]] = 0; // 初始化图中每一个顶点的完成访问时间为0
    d[vertices[i]] = 0; // 初始化图中每一个顶点的发现时间为0
    p[vertices[i]] = null; // 初始化图中每一个顶点的前溯点为null
  }
  for (let i = 0; i < vertices.length; i++) { // 再次遍历图的顶点列表，完成初始化
    if (color[vertices[i]] === Colors.WHITE) { // 如果遍历的当前项顶点是白色(该顶点还没有被访问)
      DFSVisit(vertices[i], color, d, f, p, time, adjList); // 则调用私有的递归函数深度探索顶点
    }
  }
  // 最后，返回distances对象、finished对象和predecessors对象
  return {
    discovery: d,
    finished: f,
    predecessors: p
  };
};

/**
 * 使用DFS实现拓扑排序
 */

graph = new Graph(true); // 有向图
myVertices = ['A', 'B', 'C', 'D', 'E', 'F'];
for (i = 0; i < myVertices.length; i++) {
  graph.addVertex(myVertices[i]);
}
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('B', 'D');
graph.addEdge('B', 'E');
graph.addEdge('C', 'F');
graph.addEdge('F', 'E');
const result = DFS(graph);

/**
distances: { A:1, B:11, C:2, D:8, E:4, F:3 }
finished: { A:10, B: 12, C:7, D:9, E:5, F:6 }
predecessors: [A: null, B: null, C: "A", D: "A", E: "B", F: "C"]
顶点A的发现时间为1,完成访问时间是10，前溯点为null
顶点B的发现时间为11，完成访问时间是12，前溯点为null
顶点C的发现时间为2，完成访问时间是7，前溯点为A
顶点D的发现时间为8，完成访问时间是9，前溯点为A
顶点E的发现时间为4，完成访问时间是5，前溯点为B
顶点F的发现时间为3，完成访问时间是6，前溯点为C
  */

const fTimes = result.finished; // 图的每个顶点的完成访问的时间
let s = ''; // 用于输出排序的字符串
for (let count = 0; count < myVertices.length; count++) { // 遍历图的顶点列表
  let max = 0; // 初始化max变量存储最大的顶点完成访问时间
  let maxName = null; // 初始化maxName变量存储完成访问时间最大的顶点
  for (i = 0; i < myVertices.length; i++) { // 再次遍历图的顶点列表
    if (fTimes[myVertices[i]] > max) { // 如果当前顶点的完成访问时间大于max
      max = fTimes[myVertices[i]]; // 设置max为当前顶点的完成访问时间
      maxName = myVertices[i]; // 设置maxName为当前顶点
    }
  }
  s += ' - ' + maxName; // 向字符串追加顶点
  delete fTimes[maxName]; // 从图的完成访问时间对象中删除当前顶点
}
console.log(s);
 /**
  * 最终输出结果(依据图顶点的完成访问时间大小倒序排列)
  * B - A - D - C - F - E
  */

算法

深度优先搜索

https://sothx.com/2021/04/23/DepthFirstSearch/

作者

Sothx

发布于

2021年4月23日

许可协议

图的最短路径算法-Dijkstra算法上一篇

广度优先搜索下一篇