广度优先搜索

什么广度优先搜索(BFS)

和树(Tree)的数据结构一样，我们也可以访问图(Graph)的所有节点。

广度优先搜索（breadth-first search，BFS）是搜索图的算法之一。

图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环，等等。

广度优先搜索会指定一个顶点，从这个顶点开始遍历图结构，遍历时先访问这个顶点的相邻顶点，然后再按队列的顺序访问相邻顶点的下一层顶点，直到到达要搜索的目标或者搜索完所有的点。

广度优先搜索是”先宽后深地访问顶点”的图搜索算法。

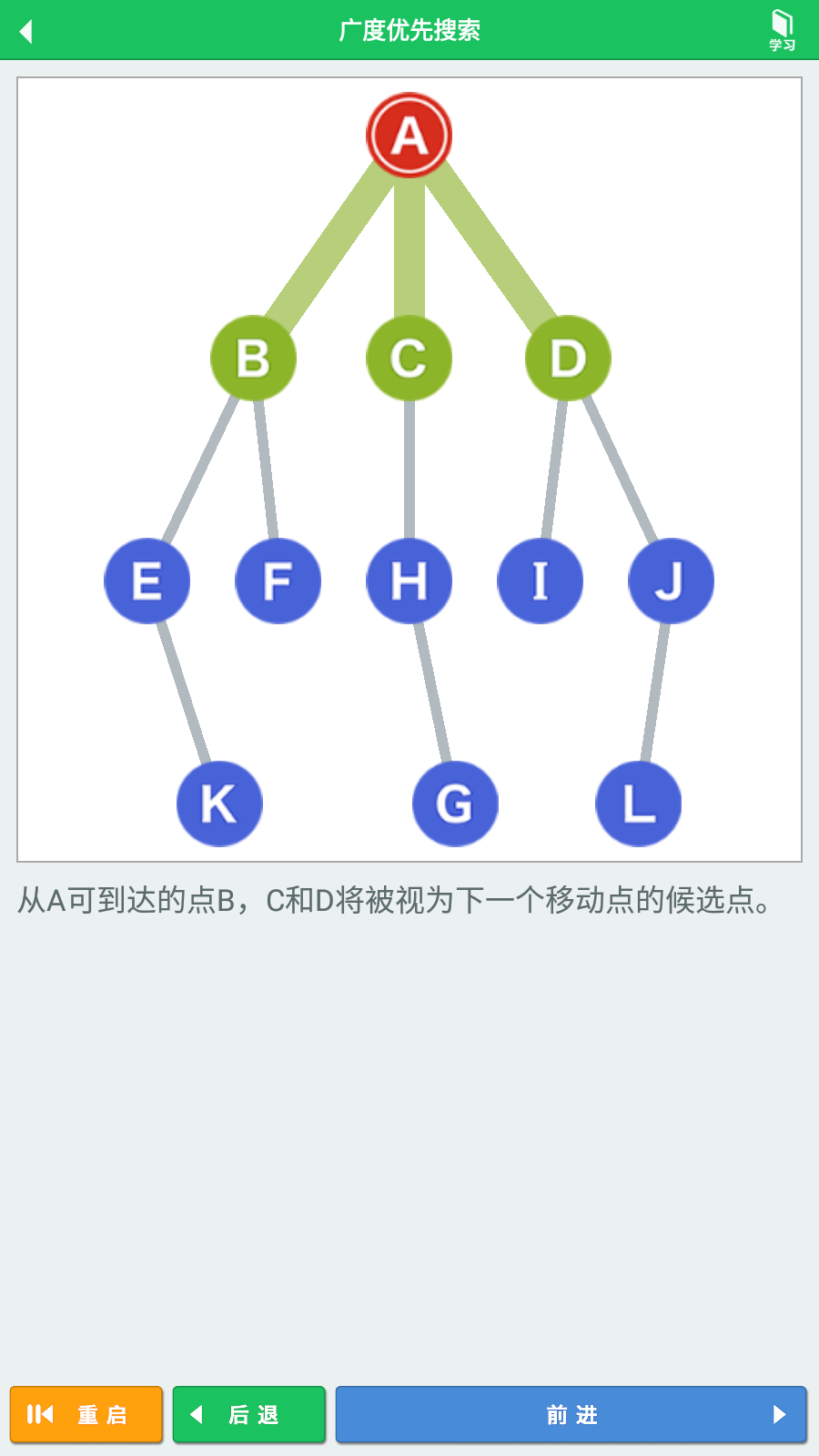
广度优先搜索(BFS)全过程

例如用下面的图结构，从顶点A开始搜索，直到搜索到顶点G。

可以知道，顶点A的相邻顶点有顶点B、顶点C、顶点D，这三个顶点，将它们视为开始搜索的顶点，加入队列。

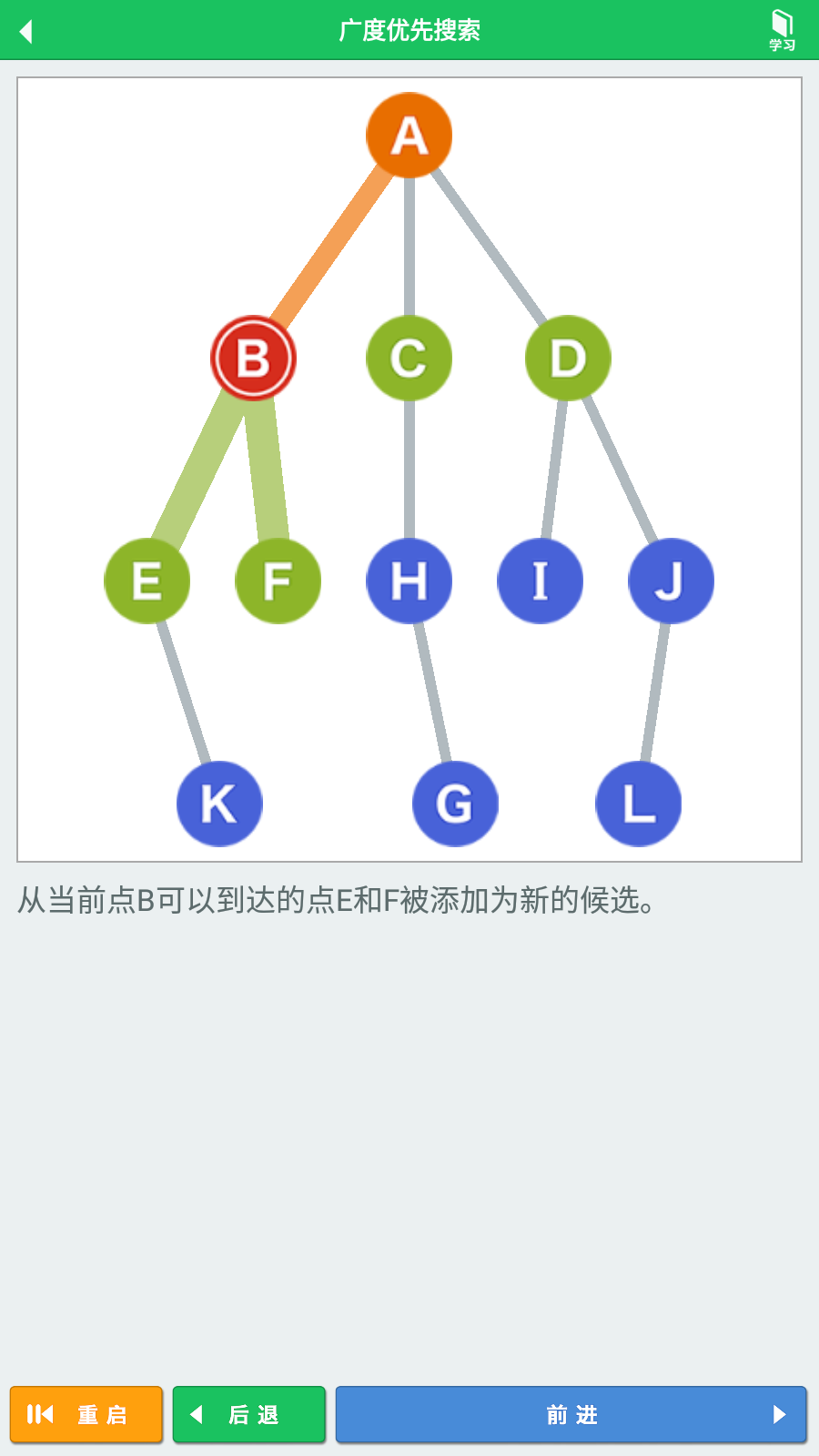
根据队列数据结构(先进先出-FIFO)的原则，我们从顶点A的三个相邻顶点(B-C-D)中，选择最先进入队列的顶点B，移动到顶点B。

获取顶点B的相邻顶点(E-F),将他们加入队列。

根据队列的顺序，使用同样的方式:

到达顶点C，获取顶点C的相邻顶点(H)，将它加入队列，接着(根据队列先进先出的原则)移动到顶点D。

获取顶点D的相邻顶点(I-J)，将它加入队列，接着(根据队列先进先出的原则)移动到顶点E。

获取顶点E的相邻顶点(K)，将它加入队列，接着(根据队列先进先出的原则)移动到顶点F。

获取顶点F的相邻顶点，发现没有相邻顶点，则进行下一个顶点H的出列。

获取顶点H的相邻顶点(G),将它加入队列，接着(根据队列先进先出的原则)移动到顶点I。

获取顶点I的相邻顶点,发现没有相邻顶点，则进行下一个顶点J的出列。

获取顶点J的相邻顶点(L),将它加入队列，接着(根据队列先进先出的原则)移动到顶点K。

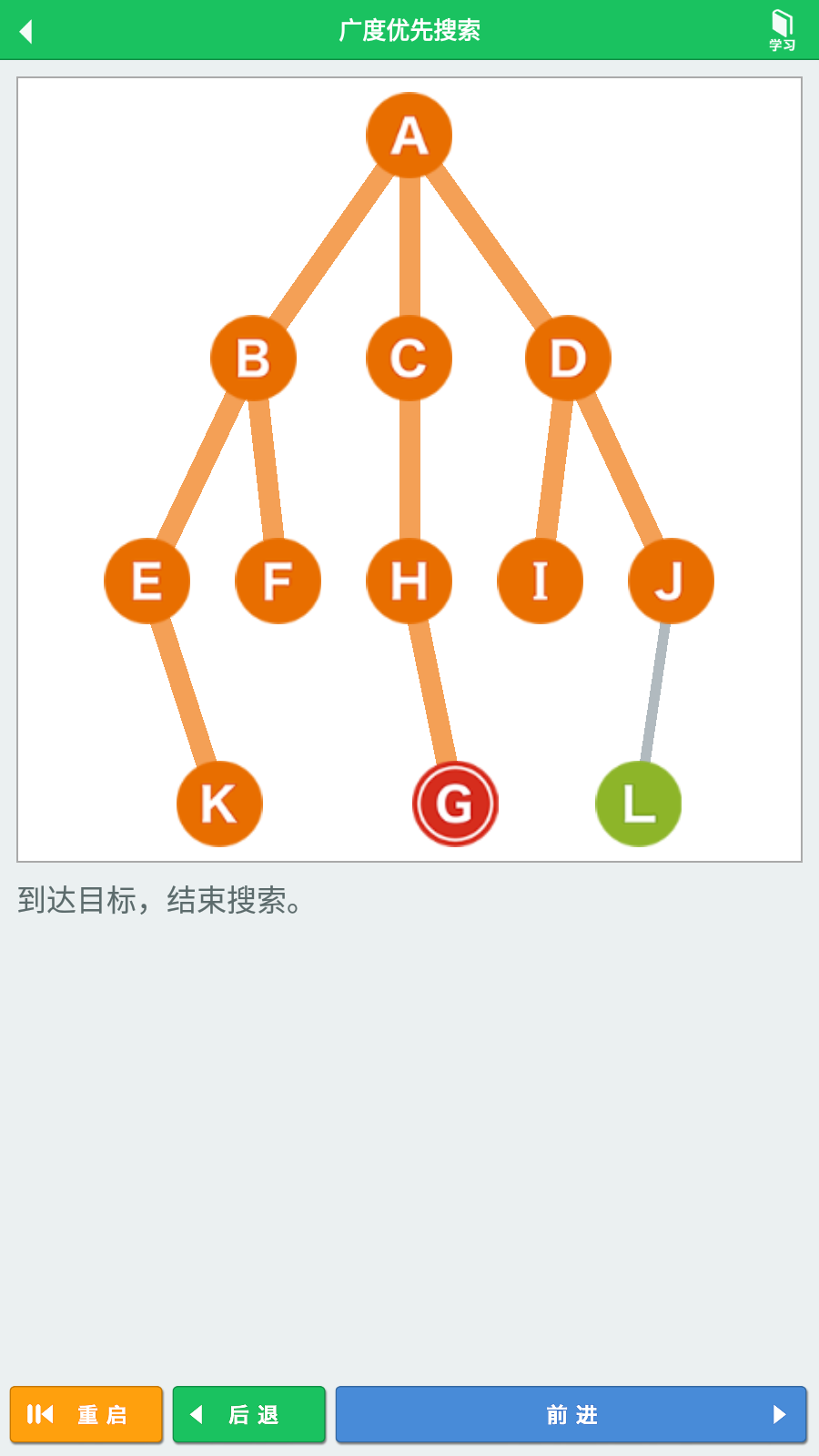
获取顶点K的相邻顶点,发现没有相邻顶点，则进行下一个顶点G的出列。

获取顶点G,找到需要到达的目标，结束搜索。

实现广度优先搜索(BFS)

代码流程

• 为了标记图的顶点，我们需要提供一个表示顶点颜色的常量对象。
  • 白色(WHITE):表示该顶点还没有被访问
  • 灰色(GREY):表示该顶点被访问过，但并未被探索过
  • 黑色(BLACK):表示该顶点被访问过且被完全探索过

// 广度优先算法中标记顶点的常量对象
const Colors = {
  WHITE: 0, // 表示该顶点还没有被访问
  GREY: 1, // 表示该顶点被访问过，但并未被探索过
  BLACK: 2 // 表示该顶点被访问过且被完全探索过
};

• 并且提供一个辅助方法，用于初始化每个顶点颜色。

/**
 * 辅助方法:初始化每个顶点的颜色的函数
 * @param {*} vertices 顶点列表
 * @returns {*} 返回初始化顶点颜色后的对象
 */
const initializeColor = vertices => {
  const color = {};
  for (let i = 0; i < vertices.length; i++) {
    color[vertices[i]] = Colors.WHITE;
  }
  return color;
};

接着便是广度优先搜索算法的完整代码思路:

• 声明广度优先搜索算法的函数-breadthFirstSearch，接收三个参数，分别是graph(要遍历的图实例)、startVertex(开始顶点)、callback(回调函数)
• 在函数内获取传入图实例(graph)的顶点列表、邻接表，并将图的顶点列表中的所有顶点初始化颜色为白色(表示该顶点还没有被访问)
• 创建一个队列数据结构实例，并将startVertex(开始顶点)入队列。
• 如果队列不为空，则进入循环，循环体内执行以下步骤:
  • 根据入队顺序，取出队列中的一个顶点，并获取这个顶点的邻接表，并将这个顶点的颜色标识为灰色(该顶点被访问过，但并未被探索过)
  • 如果这个顶点的邻接表不为空，则遍历这个顶点的邻接表中的顶点，遍历时，如果该邻接表的顶点是白色，则将它标识为灰色(该顶点被访问过，但并未被探索过),并将该邻接表顶点加入队列。
• 这个顶点的邻接表探索完后，将这个顶点标识为黑色(已被访问且被完全探索)
• 如果有传入回调函数，则执行该回调函数，回调函数会将这个顶点作为入参方法。

代码实现

/**
 * 图的广度优先搜索算法
 * 使用到的数据结构:队列
 * 概念:先宽后深地访问顶点
 * @param {*} graph 要进行遍历的图(Graph 类实例)
 * @param {*} startVertex 开始顶点
 * @param {function} callback 回调函数
 */
export const breadthFirstSearch = (graph, startVertex, callback) => {
  const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表
  const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表
  const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色
  const queue = new Queue(); // 创建一个队列实例

  queue.enqueue(startVertex); // 将开始顶点(startVertex)加入队列

  while (!queue.isEmpty()) { // 如果队列不为空，则进入循环
    const u = queue.dequeue(); // 按队列(先进先出)规则，取出队列里面存储的最前面的顶点，赋值给u
    const neighbors = adjList.get(u); // 获取顶点u的邻接表
    color[u] = Colors.GREY; // 标识顶点u为灰色(该顶点被访问过，但并未被探索过)
    for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表
      const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w
      if (color[w] === Colors.WHITE) {  // 如果当前顶点w是白色(顶点还没有被访问)
        color[w] = Colors.GREY; // 则标识顶点w为灰色(该顶点被访问过，但并未被探索过)
        queue.enqueue(w); // 将顶点w加入队列
      }
    }
    color[u] = Colors.BLACK; // 此时顶点u与其相邻顶点已经被探索，将u标识为黑色(已被访问且被完全探索)
    if (callback) { // 执行回调函数
      callback(u);
    }
  }
};

代码用例

我们初始化一个图，用于测试广度优先搜索。

let graph = new Graph();
const myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
for (let i = 0; i < myVertices.length; i++) {
    graph.addVertex(myVertices[i]);
}
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("C", "D");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("E", "I");

将这个实例图，用广度优先搜索算法打印出来。

const printVertex = (value) => console.log('Visited vertex: ' + value);
breadthFirstSearch(graph, vertices[0], printVertex);


/**
 *

// 最终打印结果
Visited vertex: A
Visited vertex: B
Visited vertex: C
Visited vertex: D
Visited vertex: E
Visited vertex: F
Visited vertex: G
Visited vertex: H
Visited vertex: I
 */

广度优先搜索算法(BFS)还可以做更多

广度优先搜索算法的工作原理了解之后，它还可以做更多事情，比如使用它来搜索图顶点的最短访问路径，或者图中某个顶点的前溯点。

下面是一段利用BFS探索图实例中每个顶点的最短路径和前溯点。

代码实现

/**
 * 使用BFS寻找图实例每个顶点最短路径和前溯点
 * @param {*} graph 要进行遍历的图(Graph 类实例)
 * @param {*} startVertex 开始顶点
 */
export const BFS = (graph, startVertex) => {
  const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表
  const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表
  const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色
  const queue = new Queue(); // 创建一个队列实例
  const distances = {}; // 存储每个顶点的距离
  const predecessors = {}; // 存储前溯点

  queue.enqueue(startVertex); // 将开始顶点(startVertex)加入队列

  for (let i = 0; i < vertices.length; i++) { // 遍历图的顶点列表 
    distances[vertices[i]] = 0; // 初始化图中每一个顶点的距离为0
    predecessors[vertices[i]] = null; // 初始化图中每一个顶点的前溯点为null
  }
  while (!queue.isEmpty()) { // 如果队列不为空，则进入循环
    const u = queue.dequeue(); // 按队列(先进先出)规则，取出队列里面存储的最前面的顶点，赋值给u
    const neighbors = adjList.get(u); // 获取顶点u的邻接表
    color[u] = Colors.GREY; // 标识顶点u为灰色(该顶点被访问过，但并未被探索过)
    for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表
      const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w
      if (color[w] === Colors.WHITE) {  // 如果当前顶点w是白色(顶点还没有被访问)
        color[w] = Colors.GREY; // 则标识顶点w为灰色(该顶点被访问过，但并未被探索过)
        distances[w] = distances[u] + 1; // 给u顶点加1来增加v和w之间的距离（u是w的前溯点，distances[u]的值已经有了）
        predecessors[w] = u; // 发现顶点u的邻点w时，则设置w的前溯点值为u
        queue.enqueue(w); // 将顶点w加入队列
      }
    }
    color[u] = Colors.BLACK; // 此时顶点u与其相邻顶点已经被探索，将u标识为黑色(已被访问且被完全探索)
  }
  // 最后，返回distances对象和predecessors对象
  return {
    distances,
    predecessors
  };
};

测试用例

我们初始化一个图，用于测试广度优先搜索。

let graph = new Graph();
const myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
for (let i = 0; i < myVertices.length; i++) {
    graph.addVertex(myVertices[i]);
}
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("C", "D");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("E", "I");

将图实例传入BFS，探索图实例中每个顶点的最短路径和前溯点。

const shortestPathA = BFS(graph, myVertices[0]);
console.log(shortestPathA.distances);
console.log(shortestPathA.predecessors);

/**
 * 
distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3]
predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E"]

距离(distances):
distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3]
顶点A到A的距离为0
顶点A到B的距离为1
顶点A到C的距离为1
顶点A到D的距离为1
顶点A到E的距离为2
顶点A到F的距离为2
顶点A到G的距离为2
顶点A到I的距离为3

前溯点(predecessors):
predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E"]
顶点A的前溯点为null
顶点B的前溯点为A
顶点C的前溯点为A
顶点D的前溯点为A
顶点E的前溯点为B
顶点F的前溯点为为B
顶点G的前溯点为C
顶点H的前溯点为D
顶点I的前溯点为E
 */

通过前溯点数组，我们还可以构建从顶点 A 到其他顶点的路径。

/**
 * 通过前溯点数组，我们还可以构建从顶点 A 到其他顶点的路径。
 */
const fromVertex = myVertices[0]; // 用顶点A作为源顶点
// 遍历除过源顶点外的顶点
for (let i = 1; i < myVertices.length; i++) {
   const toVertex = myVertices[i]; // 获取当前抵达的顶点的值
   const path = new Stack(); //  创建一个栈来存储路径值
  for (
    let v = toVertex;
    v !== fromVertex;
    v = shortestPathA.predecessors[v]
  ) {  // 追溯toVertex(当前抵达的顶点)到fromVertex(源顶点)的路径，变量v赋值为其前溯点的值
     path.push(v);  // v入栈
   }
   path.push(fromVertex); // 源顶点入栈
   let s = path.pop(); // 创建一个s字符串，并将源顶点赋值给它（它是最后一个加入栈中的，所以是第一个被弹出的项）
   while (!path.isEmpty()) { // 当栈是非空的
     s += ' - ' + path.pop(); // 从栈中移出一个项并将其拼接到字符串 s 的后面
   }
  console.log(s); // 输出路径
  // 最后，就得到了从顶点 A 到图中其他顶点的最短路径（衡量标准是边的数量）。
  /**
   * 打印结果
   *  A - B
      A - C
      A - D
      A - B - E
      A - B - F
      A - C - G
      A - D - H
      A - B - E - I 
   */
 }

完整代码实现

附上上述所有代码的完整实现

import { Queue } from '/Queue/app.js';
import { Graph } from '/Graph/app.js';

/**
 * 有两种算法可以对图进行遍历：广度优先搜索（breadth-first search，BFS）和深度优先搜索（depth-first search，DFS）。图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环，等等。
 */

// 广度优先算法中标记顶点的常量对象
const Colors = {
  WHITE: 0, // 表示该顶点还没有被访问
  GREY: 1, // 表示该顶点被访问过，但并未被探索过
  BLACK: 2 // 表示该顶点被访问过且被完全探索过
};

/**
 * 辅助方法:初始化每个顶点的颜色的函数
 * @param {*} vertices 顶点列表
 * @returns {*} 返回初始化顶点颜色后的对象
 */
const initializeColor = vertices => {
  const color = {};
  for (let i = 0; i < vertices.length; i++) {
    color[vertices[i]] = Colors.WHITE;
  }
  return color;
};
/**
 * 图的广度优先搜索算法
 * 使用到的数据结构:队列
 * 概念:先宽后深地访问顶点
 * @param {*} graph 要进行遍历的图(Graph 类实例)
 * @param {*} startVertex 开始顶点
 * @param {function} callback 回调函数
 */
export const breadthFirstSearch = (graph, startVertex, callback) => {
  const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表
  const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表
  const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色
  const queue = new Queue(); // 创建一个队列实例

  queue.enqueue(startVertex); // 将开始顶点(startVertex)加入队列

  while (!queue.isEmpty()) { // 如果队列不为空，则进入循环
    const u = queue.dequeue(); // 按队列(先进先出)规则，取出队列里面存储的最前面的顶点，赋值给u
    const neighbors = adjList.get(u); // 获取顶点u的邻接表
    color[u] = Colors.GREY; // 标识顶点u为灰色(该顶点被访问过，但并未被探索过)
    for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表
      const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w
      if (color[w] === Colors.WHITE) {  // 如果当前顶点w是白色(顶点还没有被访问)
        color[w] = Colors.GREY; // 则标识顶点w为灰色(该顶点被访问过，但并未被探索过)
        queue.enqueue(w); // 将顶点w加入队列
      }
    }
    color[u] = Colors.BLACK; // 此时顶点u与其相邻顶点已经被探索，将u标识为黑色(已被访问且被完全探索)
    if (callback) { // 执行回调函数
      callback(u);
    }
  }
};


let graph = new Graph();
const myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
for (let i = 0; i < myVertices.length; i++) {
    graph.addVertex(myVertices[i]);
}
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("C", "D");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("E", "I");

const printVertex = (value) => console.log('Visited vertex: ' + value);
breadthFirstSearch(graph, vertices[0], printVertex);


/**
 *

// 最终打印结果
Visited vertex: A
Visited vertex: B
Visited vertex: C
Visited vertex: D
Visited vertex: E
Visited vertex: F
Visited vertex: G
Visited vertex: H
Visited vertex: I
 */

/**
 * 使用BFS寻找图实例每个顶点最短路径和前溯点
 * @param {*} graph 要进行遍历的图(Graph 类实例)
 * @param {*} startVertex 开始顶点
 */
export const BFS = (graph, startVertex) => {
  const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表
  const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表
  const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色
  const queue = new Queue(); // 创建一个队列实例
  const distances = {}; // 存储每个顶点的距离
  const predecessors = {}; // 存储前溯点

  queue.enqueue(startVertex); // 将开始顶点(startVertex)加入队列

  for (let i = 0; i < vertices.length; i++) { // 遍历图的顶点列表 
    distances[vertices[i]] = 0; // 初始化图中每一个顶点的距离为0
    predecessors[vertices[i]] = null; // 初始化图中每一个顶点的前溯点为null
  }
  while (!queue.isEmpty()) { // 如果队列不为空，则进入循环
    const u = queue.dequeue(); // 按队列(先进先出)规则，取出队列里面存储的最前面的顶点，赋值给u
    const neighbors = adjList.get(u); // 获取顶点u的邻接表
    color[u] = Colors.GREY; // 标识顶点u为灰色(该顶点被访问过，但并未被探索过)
    for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表
      const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w
      if (color[w] === Colors.WHITE) {  // 如果当前顶点w是白色(顶点还没有被访问)
        color[w] = Colors.GREY; // 则标识顶点w为灰色(该顶点被访问过，但并未被探索过)
        distances[w] = distances[u] + 1; // 给u顶点加1来增加v和w之间的距离（u是w的前溯点，distances[u]的值已经有了）
        predecessors[w] = u; // 发现顶点u的邻点w时，则设置w的前溯点值为u
        queue.enqueue(w); // 将顶点w加入队列
      }
    }
    color[u] = Colors.BLACK; // 此时顶点u与其相邻顶点已经被探索，将u标识为黑色(已被访问且被完全探索)
  }
  // 最后，返回distances对象和predecessors对象
  return {
    distances,
    predecessors
  };
};

const shortestPathA = BFS(graph, myVertices[0]);
console.log(shortestPathA.distances);
console.log(shortestPathA.predecessors);

/**
 * 
distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3]
predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E"]

距离(distances):
distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3]
顶点A到A的距离为0
顶点A到B的距离为1
顶点A到C的距离为1
顶点A到D的距离为1
顶点A到E的距离为2
顶点A到F的距离为2
顶点A到G的距离为2
顶点A到I的距离为3

前溯点(predecessors):
predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E"]
顶点A的前溯点为null
顶点B的前溯点为A
顶点C的前溯点为A
顶点D的前溯点为A
顶点E的前溯点为B
顶点F的前溯点为为B
顶点G的前溯点为C
顶点H的前溯点为D
顶点I的前溯点为E
 */

/**
 * 通过前溯点数组，我们还可以构建从顶点 A 到其他顶点的路径。
 */
const fromVertex = myVertices[0]; // 用顶点A作为源顶点
// 遍历除过源顶点外的顶点
for (let i = 1; i < myVertices.length; i++) {
   const toVertex = myVertices[i]; // 获取当前抵达的顶点的值
   const path = new Stack(); //  创建一个栈来存储路径值
  for (
    let v = toVertex;
    v !== fromVertex;
    v = shortestPathA.predecessors[v]
  ) {  // 追溯toVertex(当前抵达的顶点)到fromVertex(源顶点)的路径，变量v赋值为其前溯点的值
     path.push(v);  // v入栈
   }
   path.push(fromVertex); // 源顶点入栈
   let s = path.pop(); // 创建一个s字符串，并将源顶点赋值给它（它是最后一个加入栈中的，所以是第一个被弹出的项）
   while (!path.isEmpty()) { // 当栈是非空的
     s += ' - ' + path.pop(); // 从栈中移出一个项并将其拼接到字符串 s 的后面
   }
  console.log(s); // 输出路径
  // 最后，就得到了从顶点 A 到图中其他顶点的最短路径（衡量标准是边的数量）。
  /**
   * 打印结果
   *  A - B
      A - C
      A - D
      A - B - E
      A - B - F
      A - C - G
      A - D - H
      A - B - E - I 
   */
 }