二叉堆

什么是二叉堆

二叉堆本质是一种完全二叉树，二叉堆不是最小堆就是最大堆。它能高效、快速地找出最大值和最小值，常用于优先队列和堆排序算法。

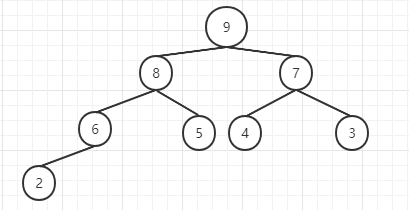
完全二叉树

完全二叉树是二叉堆的结构特性。一颗完全的二叉树，它的每一层都有左侧和右侧子节点(除最后一层的叶节点)，并且最后一层的叶节点尽可能都是左侧子节点。完全二叉树约定编号从根结点起，自上而下，自左而右进行编号。

完全二叉树是指最后一层左边是满的，右边可能满也可能不满，然后其余层都是满的二叉树称为完全二叉树。

完全二叉树

完全二叉树的比较：

例如下图a、b、c是完全二叉树，而d、e、f不是。

完全二叉树的比较

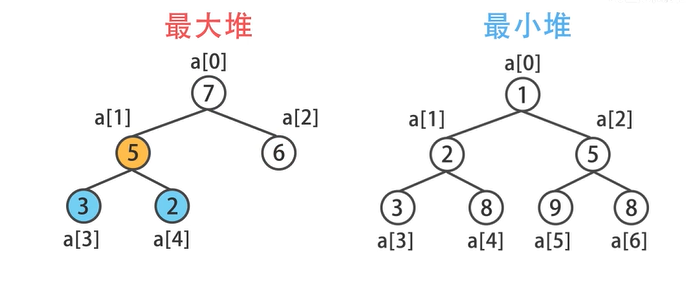
最小堆

根节点的键值是所有堆节点键值中最小的，且每个父节点的值都比子节点的值小

最大堆

根节点的键值是所有堆节点键值中最大的，且每个父节点的值都比子节点的值大

最大堆和最小堆

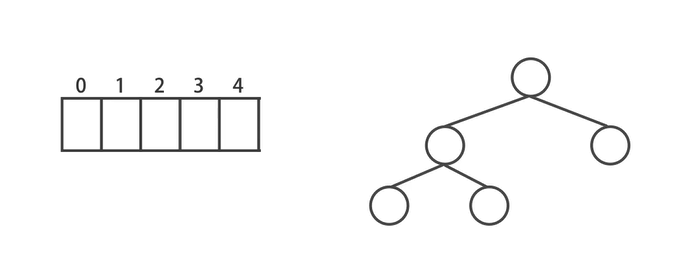
实现二叉堆

实现二叉堆有两种表示方式：

  • 像二叉树一样用指针(节点)来表示
  • 使用一个数组，通过索引值检索父节点、左侧和右侧子节点的值

二叉堆的两种表示方式

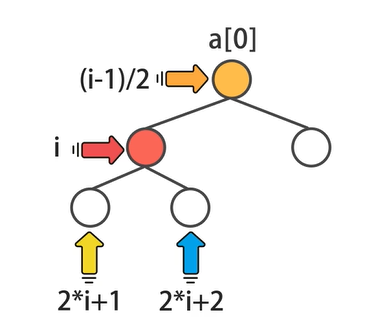
操作堆节点

对于给定位置的堆节点:

  • 它的左侧子节点位置是: 2 * index + 1 (如果位置可用)
  • 它的右侧子节点位置是: 2 * index + 2 (如果位置可用)
  • 它的父节点位置是: index / 2 (如果位置可用)

操作堆节点

定义比较函数

实现二叉堆需要与左右侧子节点、父节点进行比较，所以需要定义一组用于节点比较的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 比较用的常量对象(保证代码优雅)
export const Compare = {
  LESS_THAN: -1, // 如果第一个元素小于第二个元素，它就返回-1
  BIGGER_THAN: 1, // 如果第一个元素大于第二个元素，它就返回1
  EQUALS: 0 // 如果元素有相同的引用，它就返回 0
};

// 反转后的比较方法(用于最大堆)
export function reverseCompare(compareFn) {
  return (a, b) => compareFn(b, a);
}


// 比较用的方法
export function defaultCompare(a, b) {
  // 如果元素有相同的引用，它就返回 0
  if (a === b) {
    return Compare.EQUALS;
  }
  // 如果第一个元素小于第二个元素，它就返回-1,否之返回1
  return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}

实现最小堆

声明最小堆类

1
2
3
4
5
6
7
8
9
10
/**
 * 最小堆类
 * 根节点的键值是所有堆节点键值中最小的，且每个父节点的值都比子节点的值小。
 */
export class MinHeap {
  constructor(compareFn = defaultCompare) {
    this.compareFn = compareFn; // 默认比较方法
    this.heap = []; // 堆通常使用数组来存储数据(也可以像一般二叉树那样用指针表示)
  }
}

声明操作堆节点的方法

对于给定位置的堆节点，它的左侧子节点位置是: 2 * index + 1 (如果位置可用)

1
2
3
4
5
6
7
8
9
/**
   * 获取堆指定位置的左侧子节点的位置(index)
   * @param {number} index 需要获取的指定位置
   * @returns {number} 返回堆指定位置的左侧子节点的位置(index)
   */
  getLeftIndex(index) {
    // 二叉堆的左侧子节点的位置是 2 * index + 1（如果位置可用）
    return (2 * index) + 1;
  }

对于给定位置的堆节点，它的右侧子节点位置是: 2 * index + 2 (如果位置可用)

1
2
3
4
5
6
7
8
9
/**
   * 获取堆指定位置的右侧子节点的位置(index)
   * @param {number} index 需要获取的指定位置
   * @returns {number} 返回堆指定位置的右侧子节点的位置(index)
   */
  getRightIndex(index) {
    // 二叉堆的左侧子节点的位置是 2 * index + 2（如果位置可用）
    return (2 * index) + 2;
  }

对于给定位置的堆节点，它的父节点位置是: index / 2 (如果位置可用)

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
   * 获取堆指定位置的父节点的位置(index)
   * @param {number} index 需要获取的指定位置
   * @returns {number} 返回堆指定位置的父节点的位置(index)
   */
  getParentIndex(index) {
    // 如果获取的是根节点的位置，则它没有父节点
    if (index === 0) {
      return undefined; // 返回undefined，表示不存在
    }
    // 二叉堆的父节点位置是 index / 2（如果位置可用）
    return Math.floor((index - 1) / 2);
  }

获取堆的大小

1
2
3
4
5
6
7
/**
   *  获取二叉堆的大小
   * @returns {number} 返回二叉堆的大小
   */
  size() {
    return this.heap.length;
  }

获取堆是否为空

1
2
3
4
5
6
7
/**
   *  获取二叉堆是否为空
   * @returns {boolean} 返回二叉堆是否为空，true则为空，false则不为空
   */
  isEmpty() {
    return this.size() <= 0;
  }

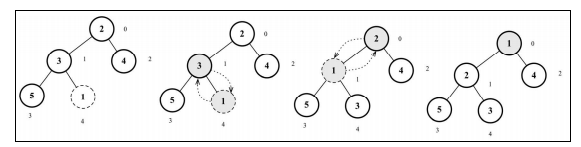
向堆中插入新数据

向堆中插入值是指将值插入堆的底部叶节点，再执行上移操作(上移操作使用的是shiftUp方法，它会将当前值与它的父节点进行交换，直到父节点小于这个插入的值)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
   * 这个方法向堆中插入一个新的值。如果插入成功，它返回 true，否则返回 false。
   * @param {number} value 需要插入到堆中的新值
   * @returns {number} 返回二叉堆的大小
   */
  insert(value) {
    if (value != null) { // 检测插入值的有效性
      const index = this.heap.length; // 保存堆的大小
      this.heap.push(value); // 将值插入堆的底部叶节点(数组的末尾)
      this.siftUp(index); // 执行上移操作方法，将这个值和它的父节点进行交换，直到父节点小于这个插入的值
      return true; // 在堆中插入新数据完成返回false
    }
    // 如果要插入的值是空的，直接返回false
    return false;
  }
上移操作(shiftUp方法)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
   * 上移操作
   * 将接收的插入值和它的父节点进行交换，直到父节点小于这个插入的值
   * @param {number} index 接收插入值的位置作为参数
   */
  siftUp(index) {
    let parent = this.getParentIndex(index); // 获取当前要插入数据的父节点位置（parent）
    while (
      index > 0 &&
      this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN
    ) { // index大于0且heap[parent] > heap[index] (第一个元素大于第二个元素)
      swap(this.heap, parent, index); // 交换parent和index位置的节点
      index = parent;  // 将当前的index索引指向新的父节点(parent)
      parent = this.getParentIndex(index); // 更新parent的值，重复这个过程进行节点交换，直到插入的值大于它的父节点(heap[parent] < heap[index])
    }
  }
交换操作(swap方法)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * 交换函数
 * @param {*} array 要操作的数组
 * @param {*} a 交换的元素位置
 * @param {*} b 被交换的元素位置
 */
export function swap(array, a, b) {
  // ES5写法(性能较好)
  /* const temp = array[a]; // 要交换数组中的两个值，我们需要声明一个临时变量temp，赋值交换的元素
  array[a] = array[b]; // 然后，将第二个元素赋值到第一个元素的位置(交换的元素赋值为被交换的元素)
  array[b] = temp; */ // 最后，将复制的第一个元素的值覆盖到第二个元素的位置(被交换的元素赋值为temp)
  // ES6写法(性能较差) https://bugzilla.mozilla.org/show_bug.cgi?id=1177319
  [array[a], array[b]] = [array[b], array[a]];
}

向堆中插入新数据

寻找堆中的最小值(最小堆)或最大值(最大堆)

  • 在最小堆中，最小值总位于数组的第一个位置(堆的根节点)
  • 在最大堆中，最大值总位于数组的第一个位置(堆的根节点)
1
2
3
4
5
6
7
/**
   * 这个方法返回最小值（最小堆）或最大值（最大堆）且不会移除这个值。
   * @returns 返回最小值（最小堆）或最大值（最大堆）
   */
  findMinimum() {
    return this.isEmpty() ? undefined : this.heap[0];
  }

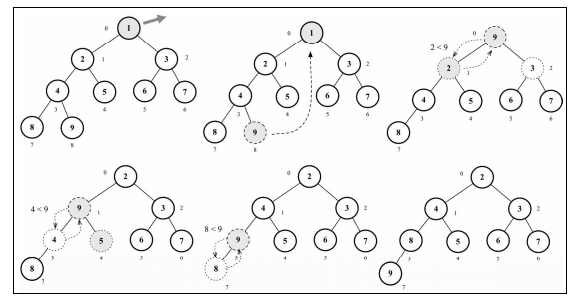
导出堆的最小值(最小堆)或最大值(最大堆)

移除最小值（最小堆的根节点）或最大值（最大堆的根节点），在移除后，将堆的最后一个元素移动至根节点，并执行下移操作(下移操作使用的是 siftDown 方法，它将交换元素直到堆的结构正常)，最后返回被移除的最小值(最小堆)或最大值(最大堆)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
   * 这个方法移除最小值（最小堆）或最大值（最大堆），并返回这个值。
   * @returns {number} 返回被移除的最小值（最小堆）或最大值（最大堆）
   */
  extract() {
    if (this.isEmpty()) { // // 如果堆为空，也就是没有值可以导出
      return undefined; // 那么我们可以返回 undefined
    }
    if (this.size() === 1) { // 如果堆的长度为1，直接返回堆顶元素
      return this.heap.shift(); // 我们可以直接移除并返回它
    }
    // 否则，声明一个临时变量保存堆顶元素
    const removedValue = this.heap[0]; // 将第一个值存储到临时变量(用于返回)
    this.heap[0] = this.heap.pop(); // 将堆最末尾的值进行移除，放置到堆头
    this.siftDown(0); // 传入堆的顶部(index为0)，执行下移操作调整堆结构
    return removedValue; // 返回刚才保存的堆顶元素
  }
下移操作(siftDown方法)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
   *  下移操作（堆化）
   * 下移操作表示将元素和最小子节点（最小堆）和最大子节点（最大堆）进行交换
   * @param {number} index 需要调整的元素位置(index)
   */
siftDown(index) {
    let element = index; // 声明一个变量(element)保存index
    const left = this.getLeftIndex(index); // 获取index的左测子节点(left)
    const right = this.getRightIndex(index); // 获取index的右侧子节点(right)
    const size = this.size(); // 堆的大小(size)
    if (
      left < size &&
      this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN
    ) { // 如果heap[element] > heap[left]，则更新element的值为left（left < size 用于校验index是否合法）
      element = left; // 交换元素和它的左侧子节点
    }
    if (
      right < size &&
      this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN
    ) { // 如果heap[element] > heap[right]，则更新element的值为right（left < size 用于校验index是否合法）
      element = right; // 交换元素和它的右侧子节点
    }
    // 交换完后判断当前保存的element和index的值是否相同，如果不相同，则未找到最小堆的位置
    if (index !== element) {
      // 如果不相同，则还未找到最小子节点的位置
      swap(this.heap, index, element); // 我们将这个元素和左/右侧子节点交换(交换index和element位置的元素)
      this.siftDown(element); // 重复这个过程(继续执行siftDown函数)
    }
  }

导出堆的最小值(最小堆)或最大值(最大堆)

清空整个堆

1
2
3
4
5
6
##/**
   *  重置整个堆
   */
  clear() {
    this.heap = [];
  }

实现最大堆

最大堆的算法和最小堆的双发一模一样，不同在于节点的比较，因此我们实现最大堆可以通过继承最小堆的堆类，将比较反转，不将a和b进行比较，而是将b和a进行比较。

创建最大堆类

1
2
3
4
5
6
7
8
9
10
11
/**
 * 最大堆类
 * MaxHeap 类的算法和 MinHeap 类的算法一模一样。不同在于节点的比较，因此我们实现最大堆可以通过继承最小堆的堆类，将比较反转，不将a和b进行比较，而是将b和a进行比较。
 */
export class MaxHeap extends MinHeap {
  constructor(compareFn = defaultCompare) {
    super(compareFn);
    this.compareFn = compareFn;
    this.compareFn = reverseCompare(compareFn);
  }
}

反转比较函数

1
2
3
4
// 反转后的比较方法(用于最大堆)
export function reverseCompare(compareFn) {
  return (a, b) => compareFn(b, a);
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
// 比较用的常量对象(保证代码优雅)
export const Compare = {
  LESS_THAN: -1, // 如果第一个元素小于第二个元素，它就返回-1
  BIGGER_THAN: 1, // 如果第一个元素大于第二个元素，它就返回1
  EQUALS: 0 // 如果元素有相同的引用，它就返回 0
};

// 反转后的比较方法(用于最大堆)
export function reverseCompare(compareFn) {
  return (a, b) => compareFn(b, a);
}


// 比较用的方法
export function defaultCompare(a, b) {
  // 如果元素有相同的引用，它就返回 0
  if (a === b) {
    return Compare.EQUALS;
  }
  // 如果第一个元素小于第二个元素，它就返回-1,否之返回1
  return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
/**
 * 交换函数
 * @param {*} array 传入需要交换的数组(这里传入堆)
 * @param {*} a 传入要交换的节点A
 * @param {*} b 传入要交换的节点B
 */
export function swap(array, a, b) {
  // ES5写法(性能较好)
  /* const temp = array[a]; // 要交换数组中的两个值，我们需要一个辅助变量来复制要交换的第一个元素
  array[a] = array[b]; // 然后，将第二个元素赋值到第一个元素的位置
  array[b] = temp; */ // 最后，将复制的第一个元素的值覆盖到第二个元素的位置
  // ES6写法(性能较差) https://bugzilla.mozilla.org/show_bug.cgi?id=1177319
  [array[a], array[b]] = [array[b], array[a]];
}

/**
 * 最小堆类
 * 根节点的键值是所有堆节点键值中最小的，且每个父节点的值都比子节点的值小。
 */
export class MinHeap {
  constructor(compareFn = defaultCompare) {
    this.compareFn = compareFn; // 默认比较方法
    this.heap = []; // 堆通常使用数组来存储数据(也可以像一般二叉树那样用指针表示)
  }
  /**
   * 获取堆指定位置的左侧子节点的位置(index)
   * @param {number} index 需要获取的指定位置
   * @returns {number} 返回堆指定位置的左侧子节点的位置(index)
   */
  getLeftIndex(index) {
    // 二叉堆的左侧子节点的位置是 2 * index + 1（如果位置可用）
    return (2 * index) + 1;
  }
  /**
   * 获取堆指定位置的右侧子节点的位置(index)
   * @param {number} index 需要获取的指定位置
   * @returns {number} 返回堆指定位置的右侧子节点的位置(index)
   */
  getRightIndex(index) {
    // 二叉堆的左侧子节点的位置是 2 * index + 2（如果位置可用）
    return (2 * index) + 2;
  }
  /**
   * 获取堆指定位置的父节点的位置(index)
   * @param {number} index 需要获取的指定位置
   * @returns {number} 返回堆指定位置的父节点的位置(index)
   */
  getParentIndex(index) {
    // 如果获取的是根节点的位置，则它没有父节点
    if (index === 0) {
      return undefined; // 返回undefined，表示不存在
    }
    // 二叉堆的父节点位置是 index / 2（如果位置可用）
    return Math.floor((index - 1) / 2);
  }
  /**
   *  获取二叉堆的大小
   * @returns {number} 返回二叉堆的大小
   */
  size() {
    return this.heap.length;
  }
  /**
   *  获取二叉堆是否为空
   * @returns {boolean} 返回二叉堆是否为空，true则为空，false则不为空
   */
  isEmpty() {
    return this.size() <= 0;
  }
  /**
   *  重置整个堆
   */
  clear() {
    this.heap = [];
  }
  /**
   * 这个方法返回最小值（最小堆）或最大值（最大堆）且不会移除这个值。
   * @returns 返回最小值（最小堆）或最大值（最大堆）
   */
  findMinimum() {
    return this.isEmpty() ? undefined : this.heap[0];
  }
  /**
   * 这个方法向堆中插入一个新的值。如果插入成功，它返回 true，否则返回 false。
   * @param {number} value 需要插入到堆中的新值
   * @returns {number} 返回二叉堆的大小
   */
  insert(value) {
    if (value != null) { // 检测插入值的有效性
      const index = this.heap.length; // 保存堆的大小
      this.heap.push(value); // 将值插入堆的底部叶节点(数组的末尾)
      this.siftUp(index); // 执行上移操作方法，将这个值和它的父节点进行交换，直到父节点小于这个插入的值
      return true; // 在堆中插入新数据完成返回false
    }
    // 如果要插入的值是空的，直接返回false
    return false;
  }
  /**
   *  下移操作（堆化）
   * 下移操作表示将元素和最小子节点（最小堆）和最大子节点（最大堆）进行交换
   * @param {number} index 需要调整的元素位置(index)
   */
  siftDown(index) {
    let element = index; // 声明一个变量(element)保存index
    const left = this.getLeftIndex(index); // 获取index的左测子节点(left)
    const right = this.getRightIndex(index); // 获取index的右侧子节点(right)
    const size = this.size(); // 堆的大小(size)
    if (
      left < size &&
      this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN
    ) { // 如果heap[element] > heap[left]，则更新element的值为left（left < size 用于校验index是否合法）
      element = left; // 交换元素和它的左侧子节点
    }
    if (
      right < size &&
      this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN
    ) { // 如果heap[element] > heap[right]，则更新element的值为right（left < size 用于校验index是否合法）
      element = right; // 交换元素和它的右侧子节点
    }
    // 交换完后判断当前保存的element和index的值是否相同，如果不相同，则未找到最小堆的位置
    if (index !== element) {
      // 如果不相同，则还未找到最小子节点的位置
      swap(this.heap, index, element); // 我们将这个元素和左/右侧子节点交换(交换index和element位置的元素)
      this.siftDown(element); // 重复这个过程(继续执行siftDown函数)
    }
  }
  /**
   * 上移操作
   * 将接收的插入值和它的父节点进行交换，直到父节点小于这个插入的值
   * @param {number} index 接收插入值的位置作为参数
   */
  siftUp(index) {
    let parent = this.getParentIndex(index); // 获取当前要插入数据的父节点位置（parent）
    while (
      index > 0 &&
      this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN
    ) { // index大于0且heap[parent] > heap[index] (第一个元素大于第二个元素)
      swap(this.heap, parent, index);  // 交换parent和index位置的节点
      index = parent;  // 将当前的index索引指向新的父节点(parent)
      parent = this.getParentIndex(index); // 更新parent的值，重复这个过程进行节点交换，直到插入的值大于它的父节点(heap[parent] < heap[index])
    }
  }
  /**
   * 这个方法移除最小值（最小堆）或最大值（最大堆），并返回这个值。
   * @returns {number} 返回被移除的最小值（最小堆）或最大值（最大堆）
   */
  extract() {
    if (this.isEmpty()) { // // 如果堆为空，也就是没有值可以导出
      return undefined; // 那么我们可以返回 undefined
    }
    if (this.size() === 1) { // 如果堆的长度为1，直接返回堆顶元素
      return this.heap.shift(); // 我们可以直接移除并返回它
    }
    // 否则，声明一个临时变量保存堆顶元素
    const removedValue = this.heap[0]; // 将第一个值存储到临时变量(用于返回)
    this.heap[0] = this.heap.pop(); // 将堆最末尾的值进行移除，放置到堆头
    this.siftDown(0); // 传入堆的顶部(index为0)，执行下移操作调整堆结构
    return removedValue; // 返回刚才保存的堆顶元素
  }
  /**
   * 数组建堆
   * @param {array} array 传入需要建成堆的数组 
   * @returns {array} 返回建好的堆
   */
  heapify(array) {
    if (array) { // 如果数组存在
      this.heap = array; // 将堆设置为这个数组
    }
    const maxIndex = Math.floor(this.size() / 2) - 1; // 获取堆需要下移的最大下标数
    for (let i = 0; i <= maxIndex; i++) { // 迭代堆前半部分的下标
      this.siftDown(i); // 执行下移函数
    }
    return this.heap; // 返回建好的堆
  }
  /**
   *  将堆转换为数组
   * @returns {array} 返回堆转换的数组
   */
  getAsArray() {
    return this.heap;
  }
}

/**
 * 最大堆类
 * MaxHeap 类的算法和 MinHeap 类的算法一模一样。不同在于节点的比较，因此我们实现最大堆可以通过继承最小堆的堆类，将比较反转，不将a和b进行比较，而是将b和a进行比较。
 */
export class MaxHeap extends MinHeap {
  constructor(compareFn = defaultCompare) {
    super(compareFn);
    this.compareFn = compareFn;
    this.compareFn = reverseCompare(compareFn);
  }
}

后记

文章部分二叉堆图片来源于B站Up主:动画讲编程

数据结构
二叉堆
https://sothx.com/2021/04/12/Heap/
作者
Sothx
发布于
2021年4月12日
许可协议