自平衡树-AVL树

前言

二叉搜索树(BST)存在一个问题，如果添加的节点数多，可能会有树的一条边特别的深，这样的状态虽然也符合二叉搜索树(BST)的特性，但是查找的性能大打折扣，几乎变成了线性查找。解决二叉搜索树多次插入新节点导致的不平衡，AVL树便是其中一种方案。

AVL树(图源自公众号"程序员小灰")

什么是Adelson-Velskii-Landi 树（AVL 树）

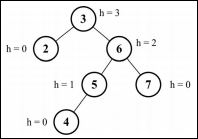
AVL树的命名取自两位发明者的首字母(G.M.Adelson-Velsky和E.M.Landis)，AVL树也被称为平衡二叉树，AVL 树是一种自平衡二叉搜索树，遵循高度平衡，添加或移除节点时，AVL树会尝试保持自平衡，它的任何一个节点左右两侧子树的高度之差最多为 1。

AVL树相关的概念

平衡因子

概念

小灰的文章有非常好的解释，我就把小灰的这段摘取过来了。

在AVL树当中，我们通过“平衡因子”来判断一颗二叉树是否符合高度平衡。

到底什么是AVL树的平衡因子呢？

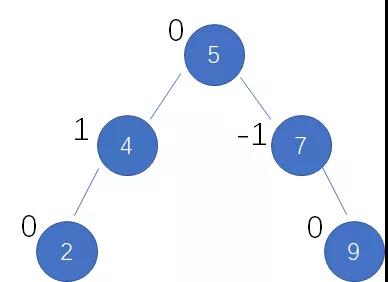
对于AVL树的每一个结点，平衡因子是它的左子树高度和右子树高度的差值。只有当二叉树所有结点的平衡因子都是-1, 0, 1这三个值的时候，这颗二叉树才是一颗合格的AVL树。

其中结点4的左子树高度是1，右子树不存在，所以该结点的平衡因子是1-0=1。

结点7的左子树不存在，右子树高度是1，所以平衡因子是0-1=-1。

所有的叶子结点，不存在左右子树，所以平衡因子都是0。

—笔记摘自公众号”程序员小灰“ 《漫画：什么是AVL树？（修订版）》

如果结果不符合上述的三个值(-1, 0, 1)之一，则需要平衡该AVL树，这就是平衡因子的概念。

AVL旋转-用于树的平衡操作

在对AVL树完成插入或者移除节点的操作后，需要计算节点的平衡因子，验证树是否需要进行平衡操作，要重新恢复AVL树的平衡操作，需要靠旋转。

AVL树的旋转有这四种场景:

左-左（LL）：向右的单旋转(右旋转)

这种情况出现于节点的左侧子节点的高度大于右侧子节点的高度时，并且左侧子节点也是平衡或左侧较重

顺时针旋转AVL树的两个结点X和Y，使得父结点被自己的左孩子取代，而自己成为自己的右孩子。

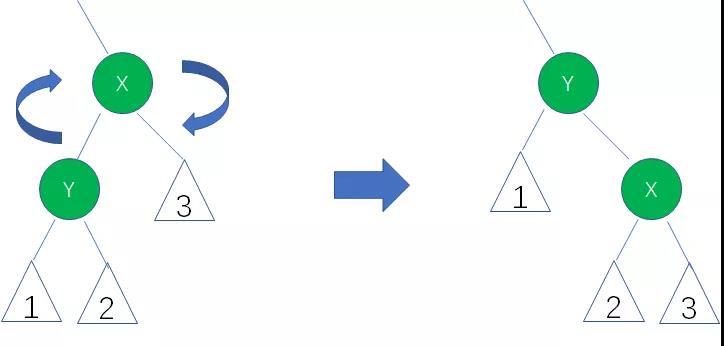
图中，身为左孩子的Y取代了X的位置，而X变成了自己的右孩子。此为右旋转。

—笔记摘自公众号”程序员小灰“ 《漫画：什么是AVL树？（修订版）》

/**
  * 左-左（LL）：向右的单旋转
  * 这种情况出现于节点的左侧子节点的高度大于右侧子节点的高度时，并且左侧子节点也是平衡或左侧较重
  * Left left case: rotate right
  *
  *       b                           a
  *      / \                         / \
  *     a   e -> rotationLL(b) ->   c   b
  *    / \                             / \
  *   c   d                           d   e
  *
  * @param node Node<T> 传入需要向右的单旋转的节点
  */
 rotationLL(node) {
   const tmp = node.left; // 将a节点置于b所在的位置
   node.left = tmp.right; // 将b节点的左子节点置为a节点的右子节点
   tmp.right = node; // 将a节点的右子节点设置为b节点
   return tmp;
 }

右-右（RR）：向左的单旋转(左旋转)

右-右的情况和左-左的情况相反。它出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点也是平衡或右侧较重的

逆时针旋转AVL树的两个结点X和Y，使得父结点被自己的右孩子取代，而自己成为自己的左孩子。说起来有些绕，见下图（标号1,2,3的三角形，是结点X和Y的子树）：

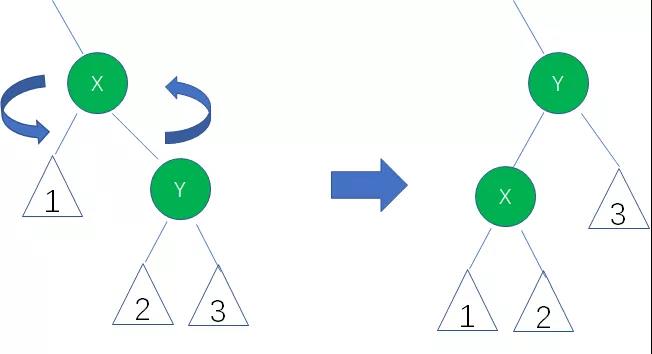
图中，身为右孩子的Y取代了X的位置，而X变成了自己的左孩子。此为左旋转。

—笔记摘自公众号”程序员小灰“ 《漫画：什么是AVL树？（修订版）》

/**
   * 右-右（RR）：向左的单旋转
   * 右-右的情况和左-左的情况相反。它出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点也是平衡或右侧较重的
   * Right right case: rotate left
   *
   *     a                              b
   *    / \                            / \
   *   c   b   -> rotationRR(a) ->    a   e
   *      / \                        / \
   *     d   e                      c   d
   *
   * @param node Node<T> 传入需要向左的单旋转的节点
   */
  rotationRR(node) {
    const tmp = node.right; // 将b节点置于a所在的位置
    node.right = tmp.left; // 将a节点的右子节点置为b节点的左子节点
    tmp.left = node; // 将b节点的左子节点设置为a节点
    return tmp;
  }

左-右（LR）：向右的双旋转（先 LL 旋转，再 RR 旋转）

这种情况出现于左侧子节点的高度大于右侧子节点的高度，并且左侧子节点右侧较重。在这种情况下，我们可以对左侧子节点进行左旋转来修复，这样会形成左-左的情况，然后再对不平衡的节点进行一个右旋转来修复

祖父结点A有一个左孩子结点B，而结点B又有一个右孩子结点C。

在这种局面下，我们先以结点B为轴，进行左旋操作：

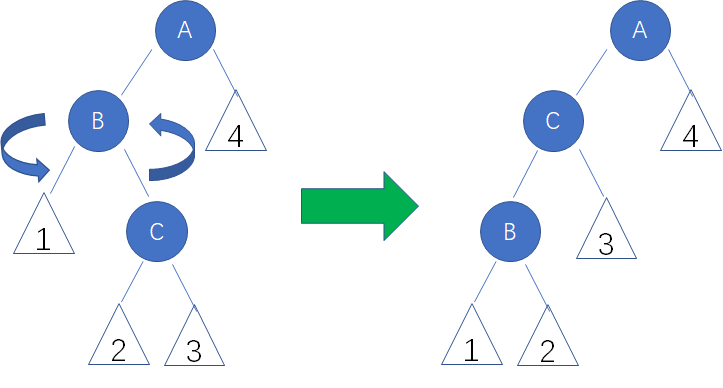
这样就转化成了左左局面。我们继续以结点A为轴，进行右旋操作：

—笔记摘自公众号”程序员小灰“ 《漫画：什么是AVL树？（修订版）》

/**
   * 左-右（LR）：向右的双旋转
   * 这种情况出现于左侧子节点的高度大于右侧子节点的高度，并且左侧子节点右侧较重。在这种情况下，我们可以对左侧子节点进行左旋转来修复，这样会形成左-左的情况，然后再对不平衡的节点进行一个右旋转来修复
   * Left right case: rotate left then right
   * @param node Node<T> 传入需要向右的双旋转的节点
   */
  rotationLR(node) {
    node.left = this.rotationRR(node.left); // 对左侧子节点进行左旋转(旋转后仍然会存在左-左的情况)
    return this.rotationLL(node); // 再对节点进行一个右旋转来修复平衡
  }

右-左（RL）：向左的双旋转（先 RR 旋转，再 LL 旋转）

右-左的情况和左-右的情况相反。这种情况出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点左侧较重。在这种情况下我们可以对右侧子节点进行右旋转来修复，这样会形成右-右的情况，然后我们再对不平衡的节点进行一个左旋转来修复

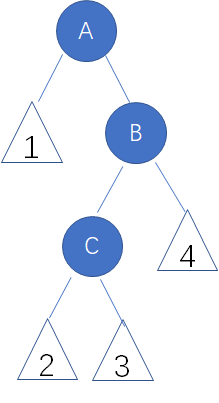
祖父结点A有一个右孩子结点B，而结点B又有一个左孩子结点C。

在这种局面下，我们先以结点B为轴，进行右旋操作：

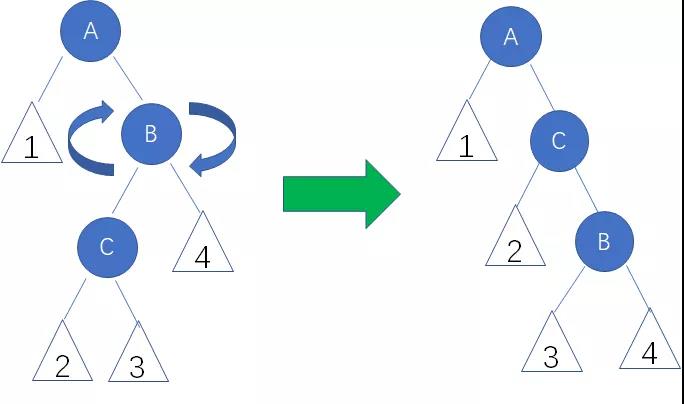
这样就转化成了右右局面。我们继续以结点A为轴，进行左旋操作：

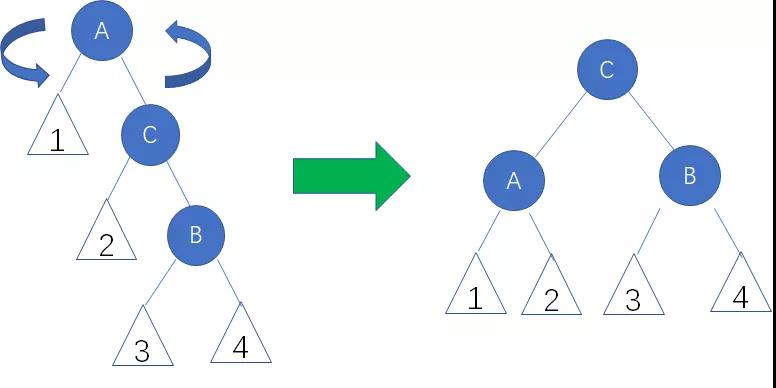
—笔记摘自公众号”程序员小灰“ 《漫画：什么是AVL树？（修订版）》

/**
   * 右-左（RL）：向左的双旋转
   * 右-左的情况和左-右的情况相反。这种情况出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点左侧较重。在这种情况下我们可以对右侧子节点进行右旋转来修复，这样会形成右-右的情况，然后我们再对不平衡的节点进行一个左旋转来修复
   * Right left case: rotate right then left
   * @param node Node<T> 传入需要向左的双旋转的节点
   */
  rotationRL(node) {
    node.right = this.rotationLL(node.right); // 对右侧子节点进行右旋转(旋转后仍然会存在右-右的情况)
    return this.rotationRR(node); // 再对节点进行一个左旋转来修复平衡
  }

代码实现

AVL树继承自BST(二叉搜索树)，实现一棵AVL树只需要重构BST(二叉搜索树)类的insert和remove方法。

import {
  Compare,
  defaultCompare,
  Node,
  BinarySearchTree
} from '/BinarySearchTree/app.js';
/**
 * AVL树是一种自平衡树。添加或移除节点时，AVL树会尝试保持自平衡。任意一个节点（不论深度）的左子树和右子树高度最多相差 1。添加或移除节点时，AVL树会尽可能尝试转换为完全树。
 */

// 平衡因子的常量对象(保证代码优雅)
export const BalanceFactor = {
  UNBALANCED_RIGHT: 1, // 右子树不平衡
  SLIGHTLY_UNBALANCED_RIGHT: 2, // 右子树稍不平衡
  BALANCED: 3, // 平衡
  SLIGHTLY_UNBALANCED_LEFT: 4, // 左子树稍不平衡
  UNBALANCED_LEFT: 5 // 左子树不平衡
};

export default class AVLTree extends BinarySearchTree {
  constructor(compareFn = defaultCompare) {
    super(compareFn);
    this.compareFn = compareFn;
    this.root = null;
  }
  /**
   * 获取节点的高度
   * @param {*} node 传入树的节点
   * @return {number} 节点的高度 -1节点高度不存在，>=0则为节点的高度
   */
  getNodeHeight(node) {
    if (node == null) { // 如果节点为空
      return -1; // 则返回-1,表示节点不存在
    }
    // 对比左侧树和右侧树的长度，获取长度最大的数，再把自身节点的长度加上，便是节点的高度
    return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1;
  }

  /**
   * 左-左（LL）：向右的单旋转
   * 这种情况出现于节点的左侧子节点的高度大于右侧子节点的高度时，并且左侧子节点也是平衡或左侧较重
   * Left left case: rotate right
   *
   *       b                           a
   *      / \                         / \
   *     a   e -> rotationLL(b) ->   c   b
   *    / \                             / \
   *   c   d                           d   e
   *
   * @param node Node<T> 传入需要向右的单旋转的节点
   */
  rotationLL(node) {
    const tmp = node.left; // 将a节点置于b所在的位置
    node.left = tmp.right; // 将b节点的左子节点置为a节点的右子节点
    tmp.right = node; // 将a节点的右子节点设置为b节点
    return tmp;
  }

  /**
   * 右-右（RR）：向左的单旋转
   * 右-右的情况和左-左的情况相反。它出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点也是平衡或右侧较重的
   * Right right case: rotate left
   *
   *     a                              b
   *    / \                            / \
   *   c   b   -> rotationRR(a) ->    a   e
   *      / \                        / \
   *     d   e                      c   d
   *
   * @param node Node<T> 传入需要向左的单旋转的节点
   */
  rotationRR(node) {
    const tmp = node.right; // 将b节点置于a所在的位置
    node.right = tmp.left; // 将a节点的右子节点置为b节点的左子节点
    tmp.left = node; // 将b节点的左子节点设置为a节点
    return tmp;
  }

  /**
   * 左-右（LR）：向右的双旋转
   * 这种情况出现于左侧子节点的高度大于右侧子节点的高度，并且左侧子节点右侧较重。在这种情况下，我们可以对左侧子节点进行左旋转来修复，这样会形成左-左的情况，然后再对不平衡的节点进行一个右旋转来修复
   * Left right case: rotate left then right
   * @param node Node<T> 传入需要向右的双旋转的节点
   */
  rotationLR(node) {
    node.left = this.rotationRR(node.left); // 对左侧子节点进行左旋转(旋转后仍然会存在左-左的情况)
    return this.rotationLL(node); // 再对节点进行一个右旋转来修复平衡
  }

  /**
   * 右-左（RL）：向左的双旋转
   * 右-左的情况和左-右的情况相反。这种情况出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点左侧较重。在这种情况下我们可以对右侧子节点进行右旋转来修复，这样会形成右-右的情况，然后我们再对不平衡的节点进行一个左旋转来修复
   * Right left case: rotate right then left
   * @param node Node<T> 传入需要向左的双旋转的节点
   */
  rotationRL(node) {
    node.right = this.rotationLL(node.right); // 对右侧子节点进行右旋转(旋转后仍然会存在右-右的情况)
    return this.rotationRR(node); // 再对节点进行一个左旋转来修复平衡
  }
  /**
   * 获取节点的平衡因子
   * 计算一个节点的平衡因子并返回其值
   */
  getBalanceFactor(node) {
    // 左子树相对右子树的高度差
    const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
    // 根据高度差，计算一个节点的平衡因子并返回其值
    switch (heightDifference) {
      case -2: // 当高度差为-2时
        return BalanceFactor.UNBALANCED_RIGHT; //返回"右子树不平衡"的常量
      case -1:
        return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT; //返回"右子树稍不平衡"的常量
      case 1:
        return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT; //返回"左子树稍不平衡"的常量
      case 2:
        return BalanceFactor.UNBALANCED_LEFT; //返回"左子树不平衡"的常量
      default:
        return BalanceFactor.BALANCED; //返回"平衡"的常量
    }
  }
  /**
   * 向树中插入一个新的键
   * @param {number} key 需要插入的新键
   */
  insert(key) {
    this.root = this.insertNode(this.root, key);
  }
  /**
   * insert的辅助方法
   * @param {*} node 传入树的根节点
   * @param {*} key 传入需要插入的新键
   * insertNode 方法会帮助我们找到新节点应该插入的正确位置
   */
  insertNode(node, key) {
    // 像在 BST 树中一样插入节点
    if (node == null) { // 检查Node类型的根节点是否为空，为空表示插入新键在第一个节点
      return new Node(key);
    }
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) { // 如果新节点的键小于当前节点的键,新键根据二叉搜索树的规则，需要插入到左侧
      node.left = this.insertNode(node.left, key); // 递归调用insertNode方法，找到节点为空的位置插入新键
    } else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) { // 如果新节点的键大于当前节点的键,新键根据二叉搜索树的规则，需要插入到右侧
      node.right = this.insertNode(node.right, key); // 递归调用insertNode方法，找到节点为空的位置插入新键
    } else { // 如果两个键的键值相等(重复)
      return node; // 直接返回，不插入新键
    }
    // 验证树是否平衡
    const balanceFactor = this.getBalanceFactor(node); // 获取节点的平衡因子计算后的常量结果
    if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) { // 如果在向左侧子树插入节点后树不平衡了
      if (this.compareFn(key, node.left.key) === Compare.LESS_THAN) { //比较是否插入的键小于左侧子节点的键
        // Left left case
        // 进行一次向右的单旋转(LL)
        node = this.rotationLL(node);
      } else {
        // 否则进行一次向右的双旋转(LR)
        // Left right case
        return this.rotationLR(node);
      }
    }
    if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) { // 如果在向右侧子树插入节点后树不平衡了
      // 在从 AVL 树中移除节点后，我们需要检查树是否需要进行平衡
      if (this.compareFn(key, node.right.key) === Compare.BIGGER_THAN) { // 比较是否插入的键小于右侧子节点的键
        // Right right case
        // 进行一次向左的单旋转(RR)
        node = this.rotationRR(node);
      } else {
        // 否则进行一次向左的双旋转(RL)
        // Right left case
        return this.rotationRL(node);
      }
    }
    return node;
  }
  /**
   * remove的辅助方法
   * @param {*} node 传入树的根节点
   * @param {*} key 传入需要删除的key值
   * removeNode 方法可以用来删除一棵树或其任意子树中的一个特定的值。
   */
  removeNode(node, key) {
    node = super.removeNode(node, key); // 以使用 BST 的 removeNode方法来从 AVL 树中移除节点
    if (node == null) {
      return node; // null，不需要进行平衡
    }
    // 检测树是否平衡
    const balanceFactor = this.getBalanceFactor(node); // 获取节点的平衡因子计算后的常量结果
    if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) { // 如果在从左侧子树移除节点后树不平衡了
      // Left left case
      if (
        this.getBalanceFactor(node.left) === BalanceFactor.BALANCED ||
        this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT
      ) { // 如果左侧节点平衡或者稍不平衡
        return this.rotationLL(node); // 进行一次向右的单旋转(LL)
      }
      // Left right case
      if (this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) { // 如果左侧子树向右稍不平衡
        return this.rotationLR(node.left); //进行一次向右的双旋转(LR)
      }
    }
    if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) { //如果在从右侧子树移除节点后树不平衡了
      // Right right case
      if (
        this.getBalanceFactor(node.right) === BalanceFactor.BALANCED ||
        this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT
      ) { // 如果右侧节点平衡或者稍不平衡
        return this.rotationRR(node); // 进行一次向左的单旋转(RR)
      }
      // Right left case
      if (this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) { // 如果右侧子树向左不平衡
        return this.rotationRL(node.right); // 进行一次向左的双旋转(RL)
      }
    }
    return node; // 返回被删除的节点
  }
}

数据结构

自平衡树-AVL树

https://sothx.com/2021/04/06/Adelson-Velskii-Landi-Tree/

作者

Sothx

发布于

2021年4月6日

许可协议

二叉堆上一篇

二叉树和二叉搜索树下一篇

自平衡树-AVL树

前言

什么是Adelson-Velskii-Landi 树（AVL 树）

AVL树相关的概念

平衡因子

概念

相关代码

AVL旋转-用于树的平衡操作

代码实现